Question

Two solid sphere of radii 2 mm and 4 mm are tied to the two ends of a light string and released in a liquid of specific gravity 1.3 and coefficient of viscosity 1 pa-s. The string is just taut, when the two spheres are completely in the liquid. If the density of the materials of the two sphere is 2800$kg{m}^{-3}$, then the terminal velocity of the system of the sphere is
(take, g = 10$m{s}^{-2}$)

Options

A. `2cms^(-1)`
B. `4cms^(-1)`
C. `4ms^(-1)`
D. `2ms^(-1)`

Answer

B

Explanation

Free body diagram of system is

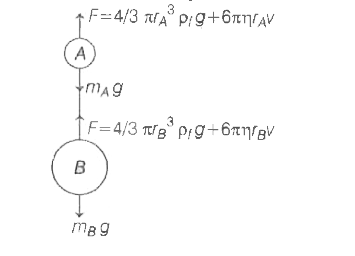
When system achieves terminal velocity,
`F_("net")=0`
`rArr4/3pirho_(f)g(r_(A)^(3)+r_(B)^(3))+6pietav(r_(A)+r_(B))=(m_(A)+m_(B))g`
With values, we get `v=4cms^(-1)`