An observer can see the topmost point of a narrow rod of height h through a small hole [Fig.2.24]. The rod is placed inside a beaker. The beaker's height is 3h and radius is h. When the beaker is filled up to 2h of its height with a liquid the observer can see the entire rod. What is the value of the refractive index of the liquid? ![An observer can see the topmost point of a narrow rod of height h through a small hole [Fig.2.24]. The rod is placed inside a beaker. The beaker's height is 3h and radius is h. When the beaker is filled up to 2h of its height with a liquid the observer can see the entire rod. What is the value of the refractive index of the liquid?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CHY_DMB_PHY_XII_P2_U06_C02_SLV_023_S01.png)
Let us assume that PQ is a thin straight rod kept in a beaker. B is a small hole on the wall of the beaker.
When the beaker is filled with a liquid up to a height 2h, then Q can be seen through the hole B.
Here QD, ray propagates through the liquid and gets refracted According to Fig. 2.55, ABRP is a square, where D is midpoint of the diagonal PB.
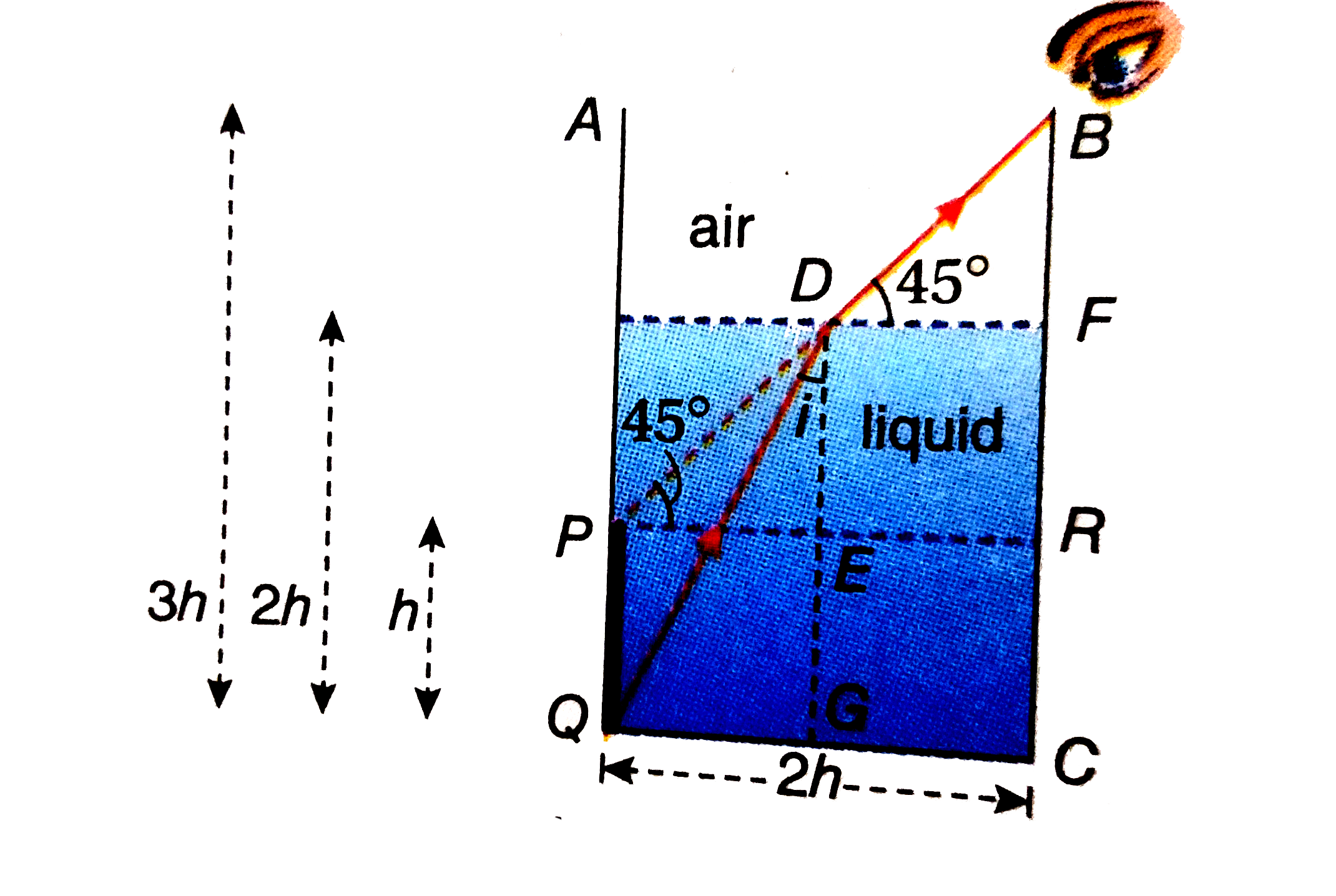
Here, DE=PE=h
Again, ∠BDF=45∘[∴∠DPE=45∘]
Since the object is placed in the denser medium, so according Snell.s law,
1μ=sinisinr=OGQDsin45∘
or, 1μ=h√5h1√2[∴QD2=QG2+GD2=h2+(2h)2=5h2]
or, 1μ=√25or,μ=√52
Therefore, required refractive index of the liquid is √52.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
An observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View SolutionAn observer can see through a small hole on the side of a jar (radius 15 cm) at a point at height of 15 cm from the bottom (see figure). The hole is at a height of 45 cm. When the jar is filled with a liquid up to a height of 30 cm the same observer can see the edge at the bottom of the jar. If the refractive index of the liquid is N/100, where N is an integer, the value of N is ___________.
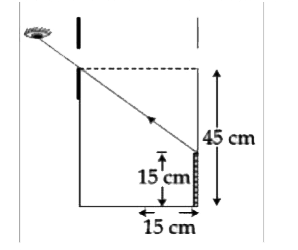
View Solution
Knowledge Check
An observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A5/2B√(5/2)C√(3/2)D3/2
A5/2B√(5/2)C√(3/2)D3/2An observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A52B√52C√32D32
A52B√52C√32D32An observer can see through a pin-hole the top end of a thin of height h, places as shown in figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A52B√52C√32D32
A52B√52C√32D32
An observer can see through a small hole on the side of a jar (radius 15 cm) at a point at height of 15 cm from the bottom (see figure). The hole is at a height of 45 cm. When the jar is filled with a liquid up to a height of 30 cm the same observer can see the edge at the bottom of the jar. If the refractive index of the liquid is N/100, where N is an integer, the value of N is ___________.

View SolutionA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
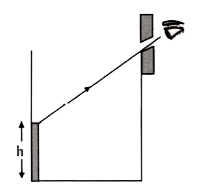
View SolutionA rod of height h is palced in a beaker of same radius. The height of the beaker is 3 times its radius. An observer sees the top end of the rod through a pin hole. When the beaker is filled with a liquid of refractive index √μ upto a height 2h, he can see the lower end of the rod. Find the value of μ
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
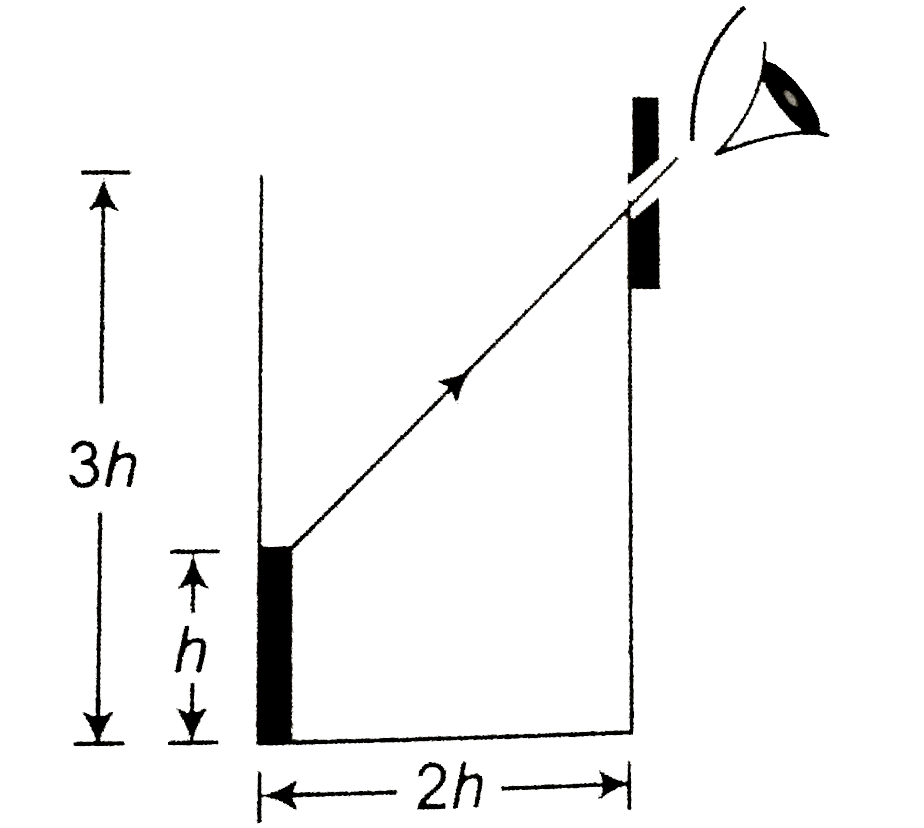
View SolutionA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
View Solution
