A glass slab is placed on a page of a book kept horizontally. What should be the value of the minimum refractive index of the glass slab so that the printed letters of the page will not be visible from any vertical side of the slab?
It is assumed that there is a thin layer of air between the page of the book and the glass slab. So ray coming from any portion of the book is incident on the glass at an angle of almost 90∘ [Fig. 2.62].
If the angle of refraction is ϕ and refractive index of glass then, sinϕ=1μ
If θc is the critical angle, then sinθc=1μ. So here, ϕ=θc
This refracted ray is incident on any vertical side of the slab at an angle θ(say).So θ+ϕ=90∘
If θ is greater than ϕ, total internal reflection of light takes place and the printed letters of te page will not be visible from any vertical side. μ will be minimum when θ=ϕ.
∴ 2ϕ=90∘or,ϕ=45∘
∴ μmin=1sinϕ=1sin45∘=√2=1.414

Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
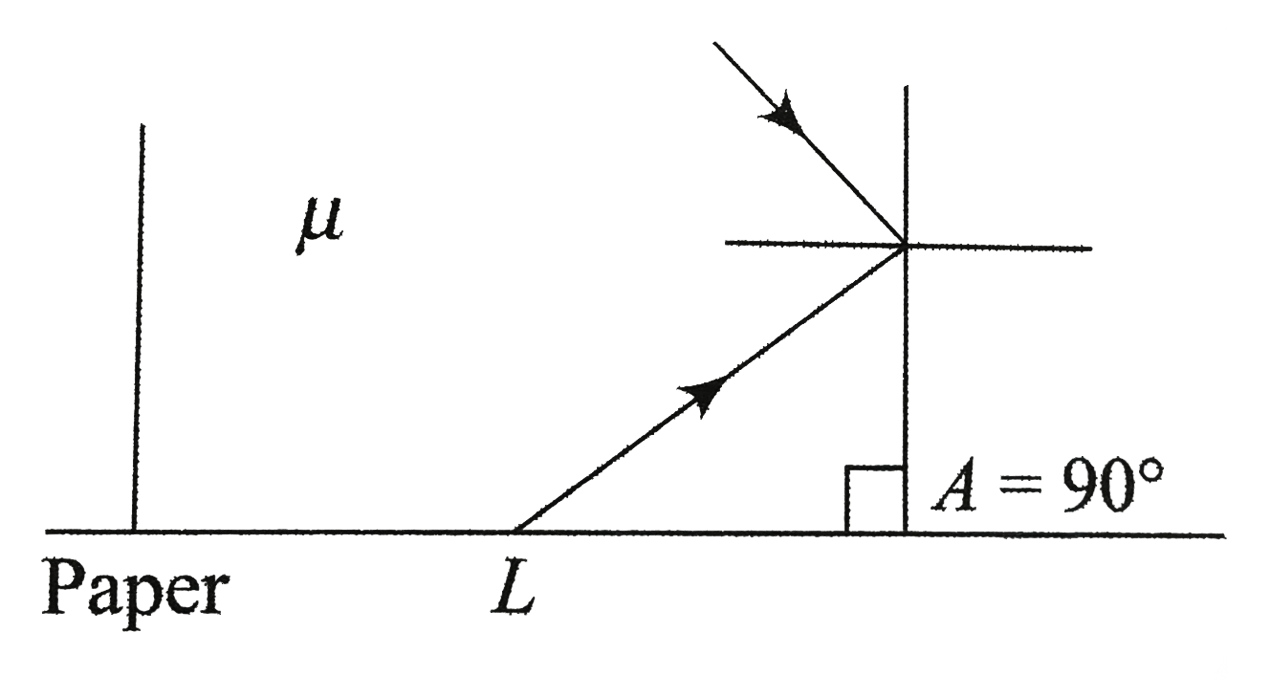
View Solution
Knowledge Check
A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
A√2B√3C√5D√5/√3Word ‘Newton’s printed on a paper and is placed on a horizontal surface below a cubical glass. The minimum value of refractive index of a cubical glass for which letters are not visible from any vertical faces, of the glass, is (Critical angle =45°)
A√3B0.5C1D√2
A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.

View SolutionTo determine refractive index of glass slab using a travelling microscope, minimum num- ber of readings required are :
View SolutionTo determine refractive index of glass slab using a travelling microscope, minimum num- ber of readings required are :
View SolutionFor a slab of flint glass, the angle of polarization is found to be 57∘24'. Calculate the refractive index of flint glass.
View SolutionA glass slab is placed over a page in which letters are printed in different colours. Will the image of all the letters lie in the same plane ?
View SolutionWhen a glass slab is placed on a dot on a paper.It apperas displaced by4cm viewed normally.What is the thickness of slab if the refractive index1.5.
View Solution
