Displacement equation for a particle moving in a straight line is x = at3+βt2+γt+δ. The ratio of the initial acceleration to the initial velocity depends only on _____ .[ Fill in the blank] Solution in Bengali
The correct Answer is:βandγ
Step by step video, text & image solution for Displacement equation for a particle moving in a straight line is x = at^(3)+betat^(2)+gammat+delta. The ratio of the initial acceleration to the initial velocity depends only on _____ .[ Fill in the blank] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - Very Short Answer Type Questions ( Graphical Analysis )5videos
ONE - DIMENSIONAL MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - Short Answer Type Questions -I5videos
ONE - DIMENSIONAL MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - EXERCISE ( Miscellaneous )3videos
ONE - DIMENSIONAL MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - CBSE SCANNER19videos
NEWTONIAN GRAVITATION AND PLANETARY MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF NEET -2017EXERCISE - QUESTION32videos
QUESTION PAPERS OF NEET -2017
Similar Questions
What is the nature of the time-displacement graph for a particle moving with a constant velocity?
02:52View SolutionCan the directions of velocity and acceleration be opposite to each other? Explain with examples.
Or,Can the velocity of a particle be towards east but its acceleration towards west?02:48View SolutionEquation of motion of a particle is x=(2t2−t3)m. Calculate the acceleration in t=2 s.
01:24View SolutionWhat is the reason for absence of atmosphere in some planets?
03:13View SolutionA molecule of a substance has permanent dipole moment p . A mole of this substance is polarised by applying a storg electrostatic field E . The direction of the field is suddenly changed of 60∘ . If N is the avogadro's number the amount of work done by the field is
01:32View SolutionThe displacement of a partical as a function of time t is given by s=α+βt+γt2+δt4, where α,β,γ and δ are constants. Find the ratio of the initial velocity to the initial acceleration.
02:52View SolutionFor a particle moving along a straight line, the displacement x depends on time t as x=αt3+βt2+γt+δ. The ratio of its initial acceleration to its initial velocity depends
02:52View SolutionFor a particle moving along a straight line, the displacement x depends on time t as x=At^(3)+Bt^(2)+Ct+D . The ratio of its initial velocity to its initial acceleration depends on:
04:25View SolutionAcceleration (a) -displacement (s) graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The v−s graph of the particle would be
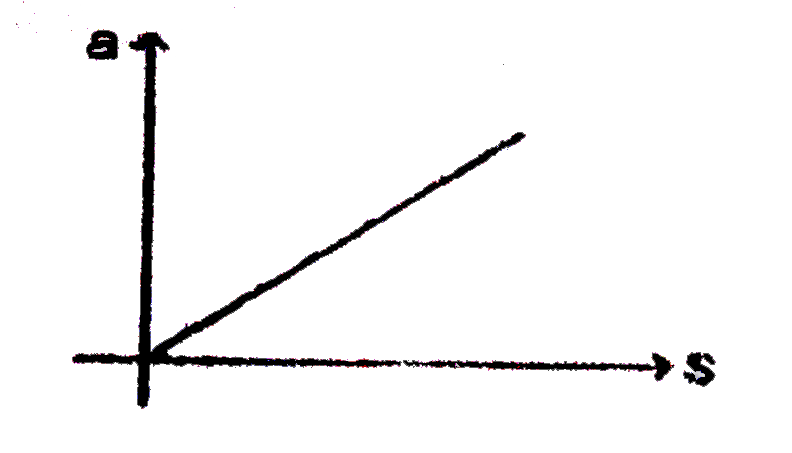 03:31View Solution
03:31View SolutionAcceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
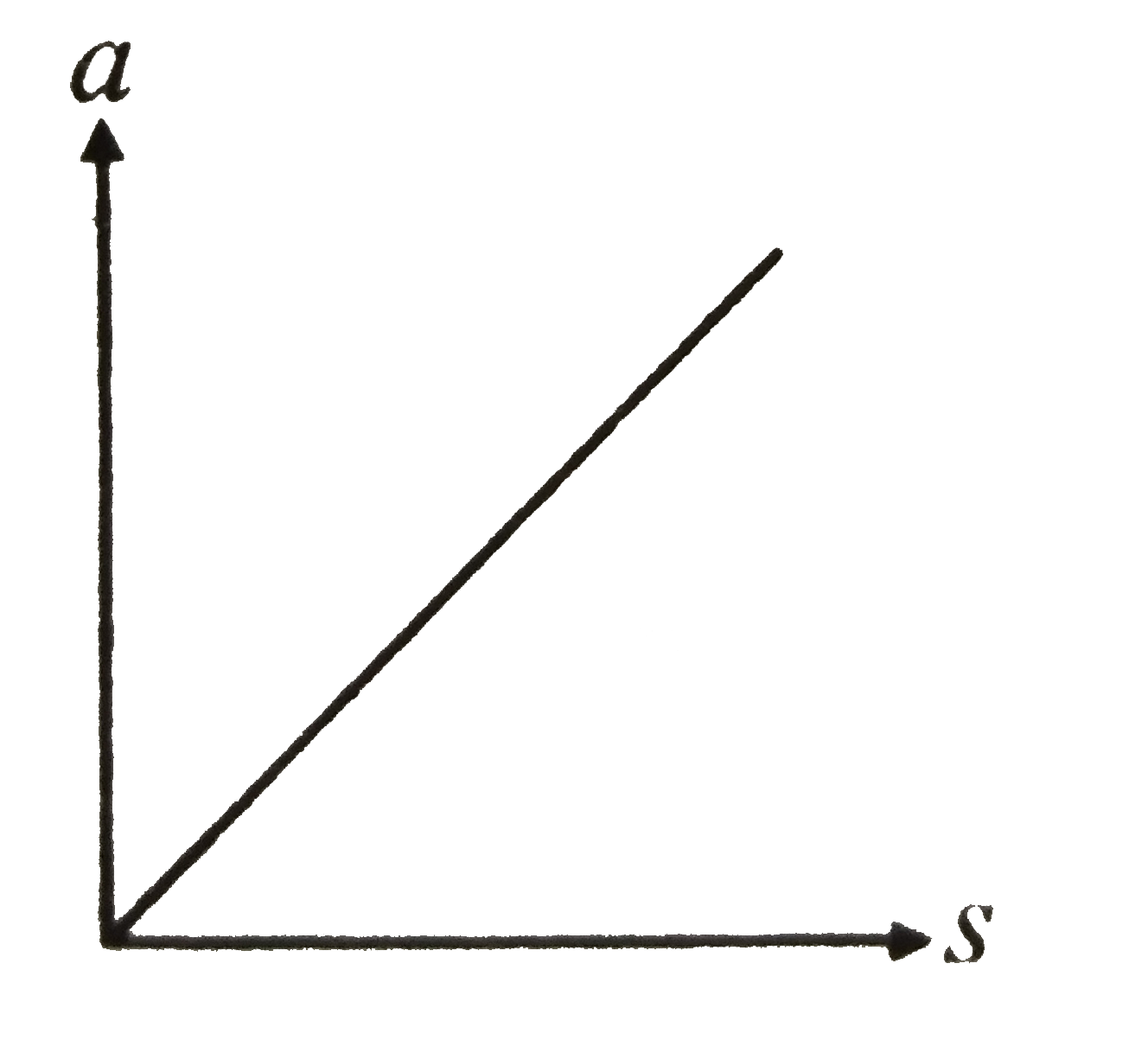 03:25View Solution
03:25View SolutionThe displacement of a particle moving in a straight line is given by the expression x=At^(3)+Bt^(2)+Ct+D in metres, where t is in seconds and A,B,C and D are constant. The ratio between the initial acceleration and initial velocity is
03:30View SolutionThe displacement of a particle moving in a straight line Is given by the expression x=At3+Bt2+Ct+Dmeters, where t is in seconds and A, B, C and D are constants. The ratio between the initial acceleration and initial velocity is
03:34View SolutionThe displacement of a particle moving along a straight line is given by
s=3t^(3)+2t^(2)-10t. find initial velocity and acceleration of particle.View SolutionDisplacement of a particle moving in a straight line is represented as follows:
x=at3+bt2+ct+d Ratio of initial velocity to initial acceleration depends.02:59View SolutionAcceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
02:14View Solution

