A particle falls from rest from the highest point of a vertical circle of radius r, along a chord without any friction . Show that the time taken by the particle to come down is independent of the chord's length. Find the time in terms of r and g .
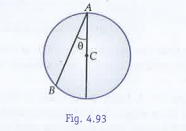
Let the chord along which the partical falls be CD
[Fig.2.67] . CD makes an angle θ with the vertical diameter as shown.
CD =2r cosθ. The component of acceleration due to gravity along CD =gcosθ . Let the time taken by this particle to fall from rest along CD be t .

Hence, from the equation s=ut+12at2,
2rcosθ=0+12gcosθ⋅t2
or,t2=4rgor,t=2√rg.
The time is independent of θ, and hence on the length of the chord CD.
Topper's Solved these Questions
- VECTORBOOK - CHHAYA PUBLICATIONCHAPTER - VECTOREXERCISE - Section Related Questions
23 Videos
- VECTORBOOK - CHHAYA PUBLICATIONCHAPTER - VECTOREXERCISE - Higher Order Thinking Skill (Hots) Questions
28 Videos
- THERMOMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - THERMOMETRYEXERCISE - EXAMINATION ARCHIEVE - WBJEE
1 Videos
- VISCOSITY AND SURFACE TENSIONBOOK - CHHAYA PUBLICATIONCHAPTER - VISCOSITY AND SURFACE TENSIONEXERCISE - EXERCISE (CBSE SCANNER)
9 Videos
Similar Questions
A particel slides from rest from the topmost point of a vertical circle of radirs r along a smooth chord making an angle θ with the vertical. The time of descent is .
View SolutionA glass marble slides from rest from the topmost point of a vertical circle of radius r along a smooth chord. Does the time of descent depend upon the chord chosen ?
View Solution
Knowledge Check
A particle slides from rest from the topmost point of a vertical circle of radius r along a smooth chord making an angle θ with the vertical. The time of descent is .
ALeast for θ=0BMaximum for θ=0CLeast for θ=45DIndependent of θA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
Amg=mv2rBmg>mv2rCmg≤mv2rDmg≥mv2rA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
A1Bfinite but largeCzeroDInfinite
A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View SolutionA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is infinite
View SolutionA smooth circular tube of radius R is fixed in a vertical plane. A particle is projectid from its lowest point with a velocity just sufficient to carry it to th ehigest point. Show that the time taken by the particle to rach the end of the horizontal diameter is (√Rg)In(1+√2) .
Hint : ∫secθ.dthη=In(secθ+tanθ)
View SolutionA smooth circular tube of radius R is fixed in a vertical plane. A particle is projectid from its lowest point with a velocity just sufficient to carry it to th ehigest point. Show that the time taken by the particle to rach the end of the horizontal diameter is (√Rg)In(1+√2) .
Hint : ∫secθ.dthη=In(secθ+tanθ)
View SolutionA particle is thrown vertically upwards from the surface of the earth. Let TP be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of TP,TQ and H, is :-
View Solution
