A particel slides from rest from the topmost point of a vertical circle of radirs r along a smooth chord making an angle θ with the vertical. The time of descent is .
Least for θ=0
Maximum for θ=0
Least for θ=45
Independent of θ
The correct Answer is:D
To solve the problem of a particle sliding from rest from the topmost point of a vertical circle of radius r along a smooth chord making an angle θ with the vertical, we can follow these steps:
1. Understanding the Setup:
- The particle starts from rest at the topmost point of a vertical circle of radius r.
- It slides down along a chord that makes an angle θ with the vertical.
2. Identifying Key Points:
- Let O be the center of the circle, P be the topmost point, and Q be the point where the particle reaches after sliding down the chord.
- The vertical distance from P to Q can be expressed in terms of r and θ.
3. Finding the Length of the Chord:
- The length L of the chord PQ can be calculated using trigonometry. In the triangle formed by points P, O, and Q, we can express L as:
L=2rcos(θ)
4. Determining the Acceleration:
- The component of gravitational acceleration acting along the chord is given by:
a=gcos(θ)
- Here, g is the acceleration due to gravity.
5. Using the Equations of Motion:
- Since the particle starts from rest, its initial velocity u=0.
- We can use the equation of motion:
s=ut+12at2
- Substituting u=0 and s=L:
L=12at2
- Substituting a=gcos(θ) and L=2rcos(θ):
2rcos(θ)=12(gcos(θ))t2
6. Solving for Time t:
- Rearranging the equation gives:
2rcos(θ)=12gcos(θ)t2
- Dividing both sides by cos(θ) (assuming θ≠90∘):
2r=12gt2
- Multiplying both sides by 2:
4r=gt2
- Finally, solving for t:
t2=4rg⇒t=2√rg
Final Result:
The time of descent t is given by:
t=2√rg
This shows that the time of descent is independent of the angle θ.
- The particle starts from rest at the topmost point of a vertical circle of radius r.
- It slides down along a chord that makes an angle θ with the vertical.
- Let O be the center of the circle, P be the topmost point, and Q be the point where the particle reaches after sliding down the chord.
- The vertical distance from P to Q can be expressed in terms of r and θ.
- The length L of the chord PQ can be calculated using trigonometry. In the triangle formed by points P, O, and Q, we can express L as:
L=2rcos(θ)
- The component of gravitational acceleration acting along the chord is given by:
a=gcos(θ)
- Here, g is the acceleration due to gravity.
- Since the particle starts from rest, its initial velocity u=0.
- We can use the equation of motion:
s=ut+12at2
- Substituting u=0 and s=L:
L=12at2
- Substituting a=gcos(θ) and L=2rcos(θ):
2rcos(θ)=12(gcos(θ))t2
- Rearranging the equation gives:
2rcos(θ)=12gcos(θ)t2
- Dividing both sides by cos(θ) (assuming θ≠90∘):
2r=12gt2
- Multiplying both sides by 2:
4r=gt2
- Finally, solving for t:
t2=4rg⇒t=2√rg
The time of descent t is given by:
t=2√rg
This shows that the time of descent is independent of the angle θ.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective
29 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A conical pendulum of length L makes an angle θ with the vertical. The time period will be

View SolutionInside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
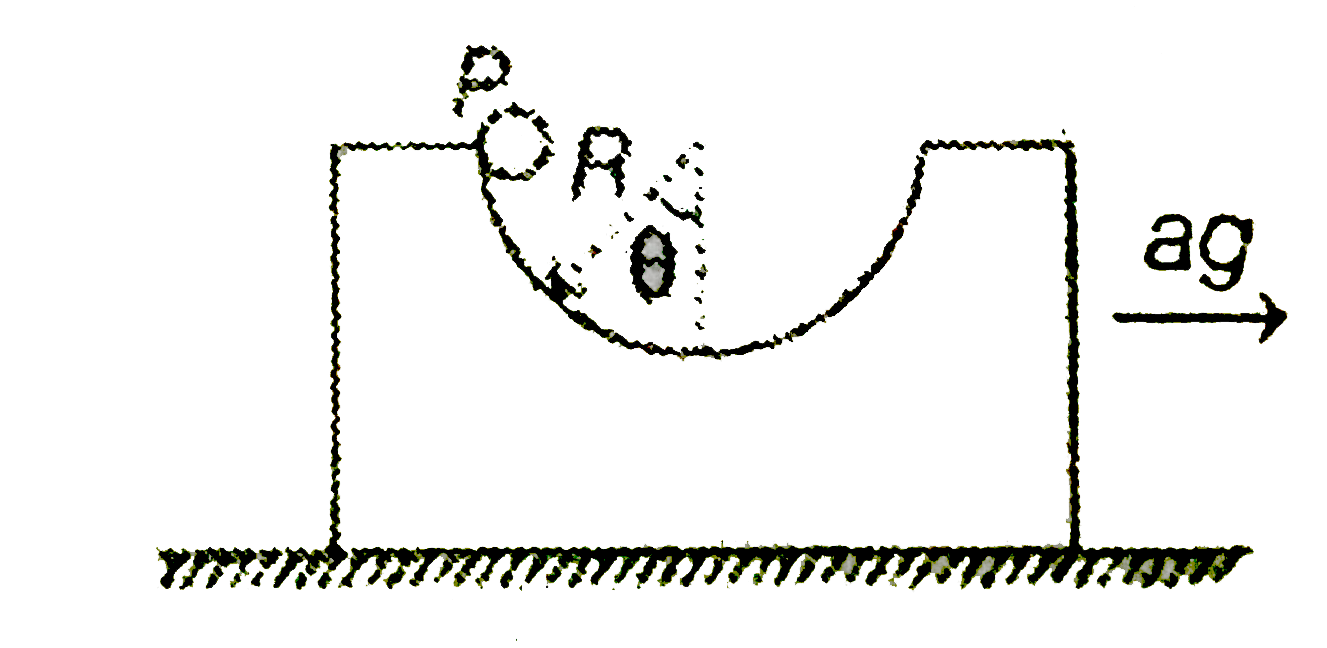
View SolutionA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is infinite
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle '/theta' with the vertical in equilibrium. Then the tension in the string is :
View SolutionWhen a cyclist negotiates a circular path of radius .r. with velocity .v., making an angle θ with the vertical, show that tanθ=v2rg.
View SolutionPQ is a smooth inclined plane whose angle θ can be varied in such a way that point Q remains fixed and P can move on a vertical line PR. A particle slides from rest from point P at different value of θ time for descent from P and Q is noted. The following statement (s) is / are correct about the time of descent :

A. the minimum time of descent is 2√l/g
B. the time descent is minimum continuously as θ is increased
C. the time of descent decreases continuously as θ is increased
D. the time of descent first decreases then increases.
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionTwo particles are projected with same initial velocity one makes angle θ with horizontal while other makes an angle θ with vertical. If their common range is R then product of their time of flight is directly proportional to :
View SolutionA block of mass m moving on a fixed smooth hemisphere of rudius R. If speed of block at top most point of the hemisohere is √gR as shown in the figure, then the angle (θ) with the vertical, where the normal contact force becomes zero will be
View Solution
