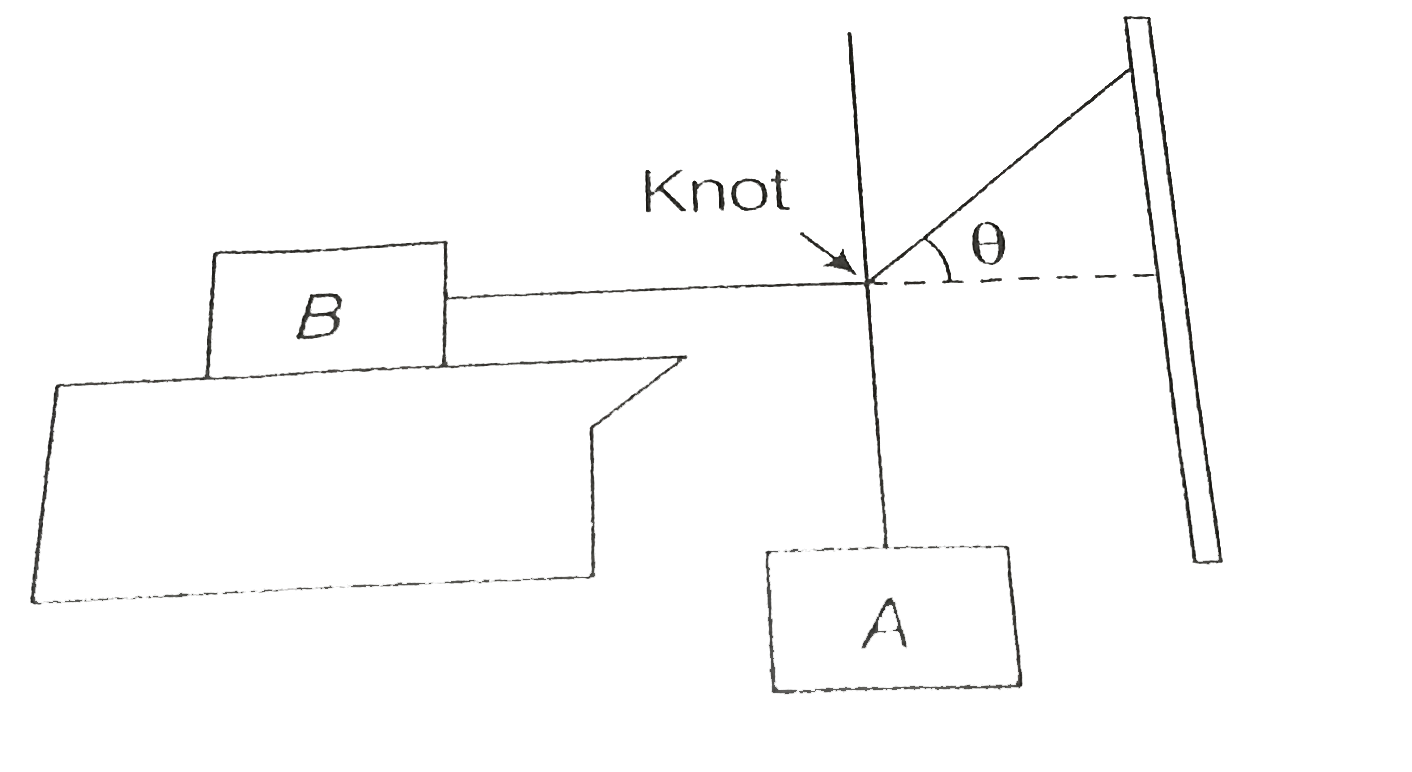
Block B lying on a table weighs W. The coefficient of static friction between the block and the table is μ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is

Wtanθμ
μWtanθ
μW√1+tan2θ
μWsinθ
The correct Answer is:B
Normal reaction of the table on block B = W So the effective frictional force acting on the left = μ W
Again when the maximum weight of A is W0, it acts downwards. Therefore when in equilibrium, the cord between the knot and the wall will be along the resultant of μW and W0.
In that case, tan θ=W0μW or,W0=μWtanθ
Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - EXAMINATION ARCHIVE with solutions ( JEE Main )
2 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - CBSE SCANNER
7 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - EXAMINATION ARCHIVE with solutions (WBCHSE )
10 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
View SolutionThe coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View Solution
Knowledge Check
Block B lying on a table weighs W. The coefficient of static friction between the block and the table is μ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
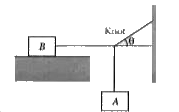 AWtanθμBμWtanθCμW√1+tan2θDμWsinθ
AWtanθμBμWtanθCμW√1+tan2θDμWsinθA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θThe system shown is just on the verge of slipping. The coefficient of static friction between the block and the table top is :
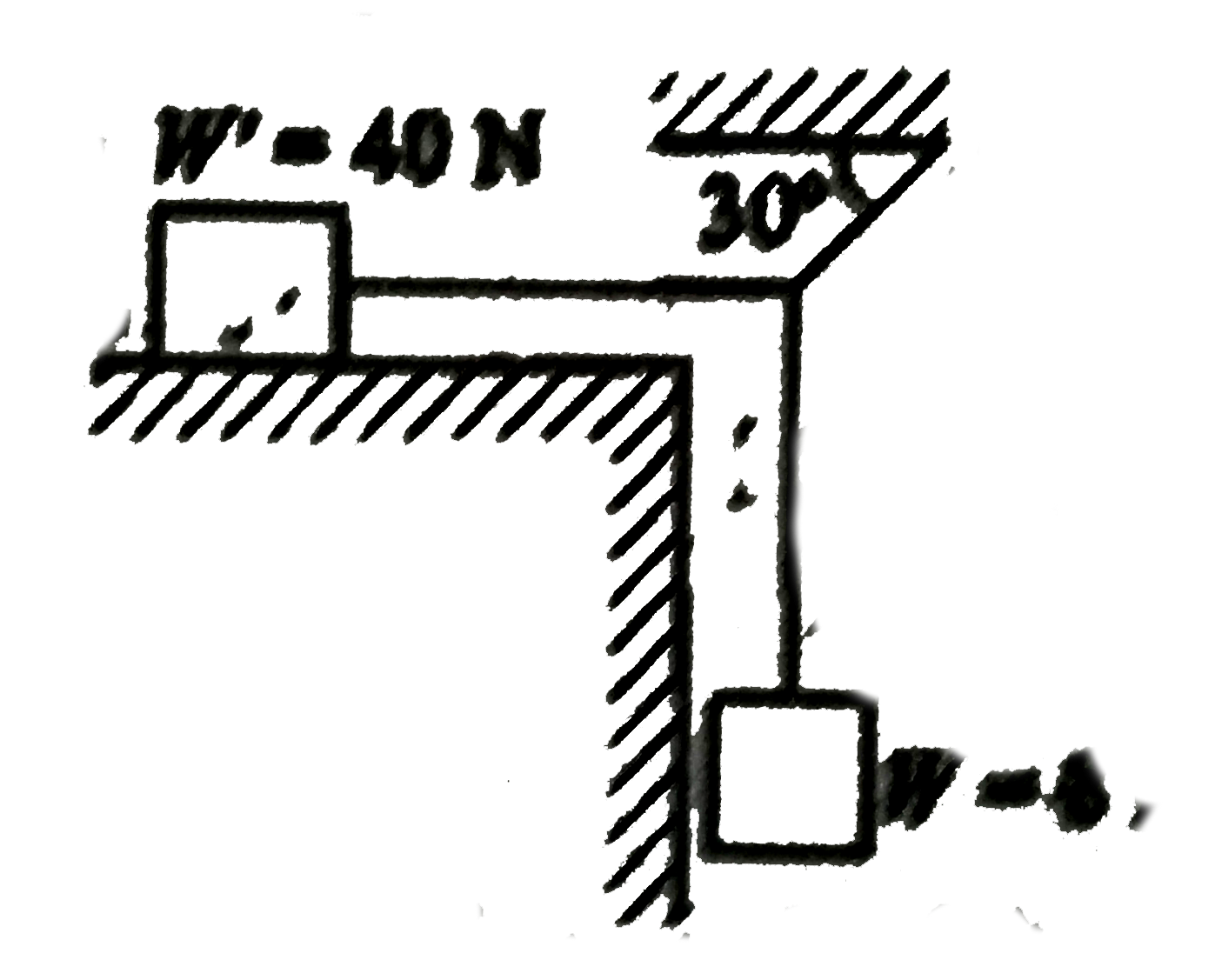 A0.5B0.95C0.15D0.35
A0.5B0.95C0.15D0.35
The coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View Solutiona. Block A , as shown in figure weight 60.0N The coefficient of static friction between the block and the surface on which it rest is 0.25 .The system is in equlibrium .Find the friction for excerted on block A
b. Find the maximum weight w for which the system will remain in equlibrium
View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
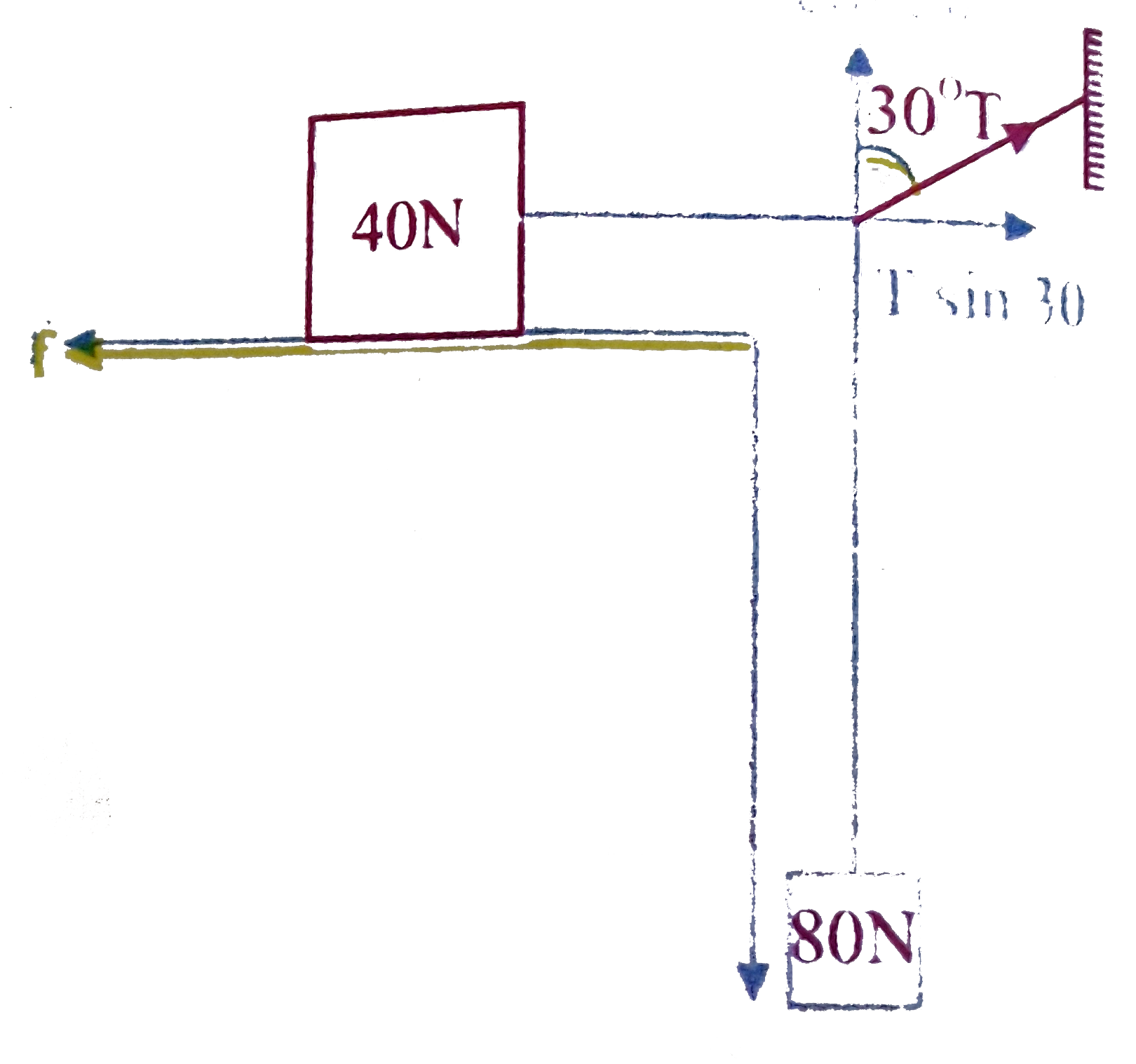 .
.
View SolutionThe coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
