A carpet of mass M made of inextensible material is rolled along its length in the form of a cylinder of radius R and is kept on a rough floor. The carpet starts unrolling without sliding on the floor when a negligibly small push is given to it. Calculate the horizontal velocity of the axis of the cylindrical part of the carpet when its radius reduces to R2.
The correct Answer is:2.16√gR
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - ENTRANCE CORNER
5 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - MULTIPLE CORRECT ANSWER TYPE
2 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - PROBLEM SET - II
20 Videos
- CALORIMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - CALORIMETRYEXERCISE - EXAMINATION ARCHIVE
5 Videos
- DOPPLER EFFECT IN SOUND BOOK - CHHAYA PUBLICATIONCHAPTER - DOPPLER EFFECT IN SOUND EXERCISE - CBSE SCANNER
2 Videos
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View Solution
Knowledge Check
A floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
A25MgRB57MgRC78MgRDMgRA floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
A1. 12MgRB2. 78MgRC3. 58MgRD4. 34MgRA uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
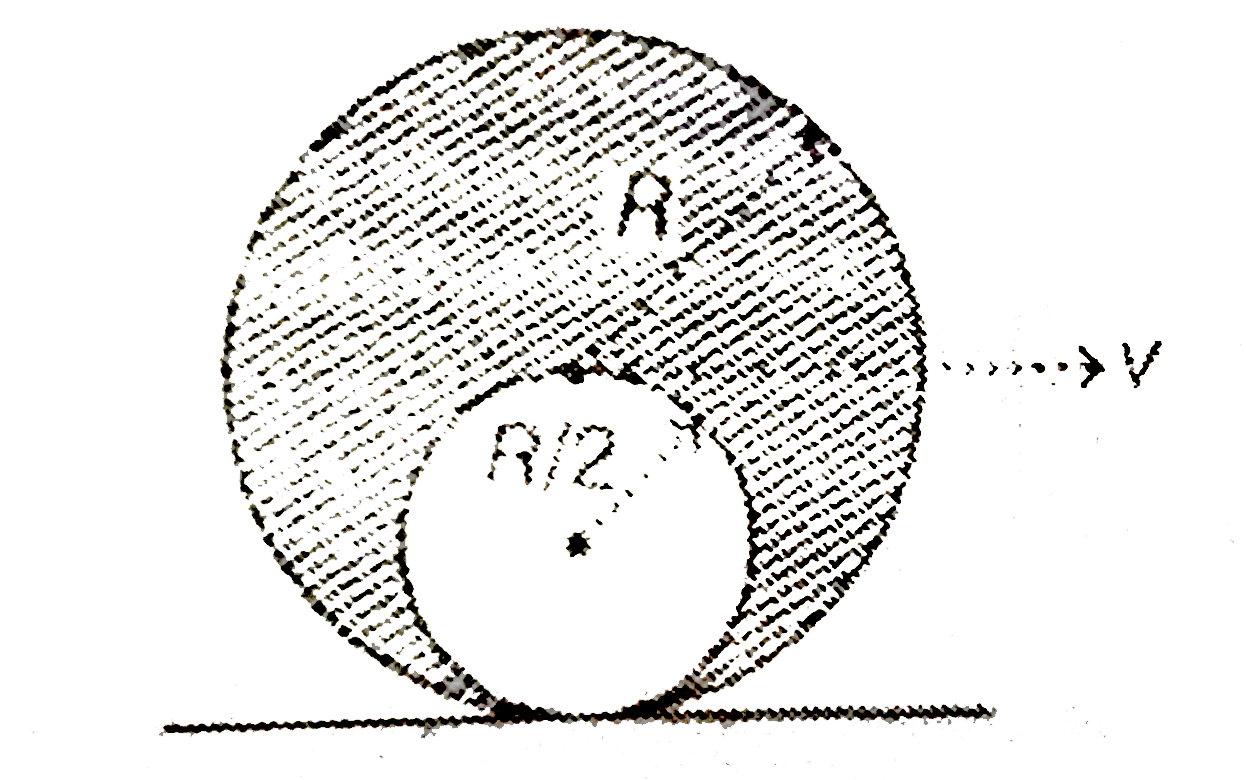 ATotal kinetic energy at this moment is 1516Mv2BTotal kinetic energy at this moment is 159Mv2CVelocity of centre of mass of the cylinder at this moment is 43vDVelocity of centre of mass of the cylinder at this moment is 76v
ATotal kinetic energy at this moment is 1516Mv2BTotal kinetic energy at this moment is 159Mv2CVelocity of centre of mass of the cylinder at this moment is 43vDVelocity of centre of mass of the cylinder at this moment is 76v
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
View SolutionA uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
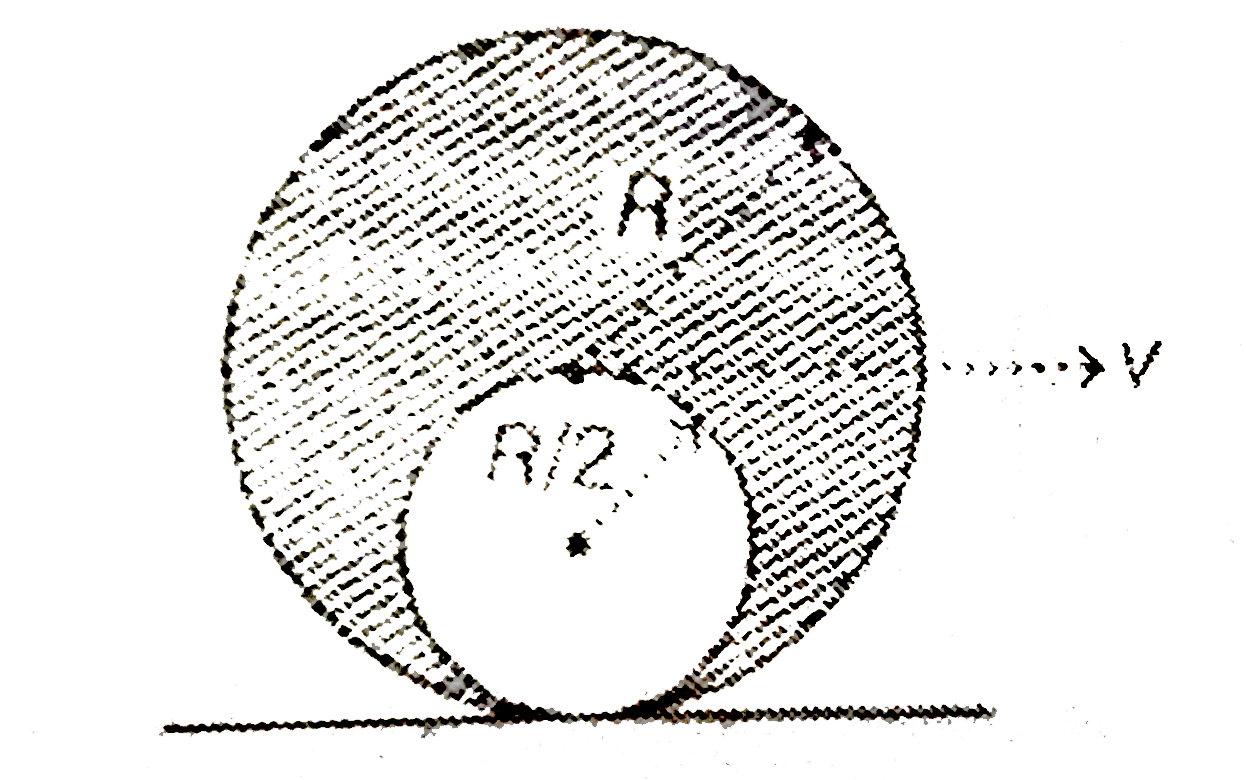
View SolutionA sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionA uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
View Solution
