Question

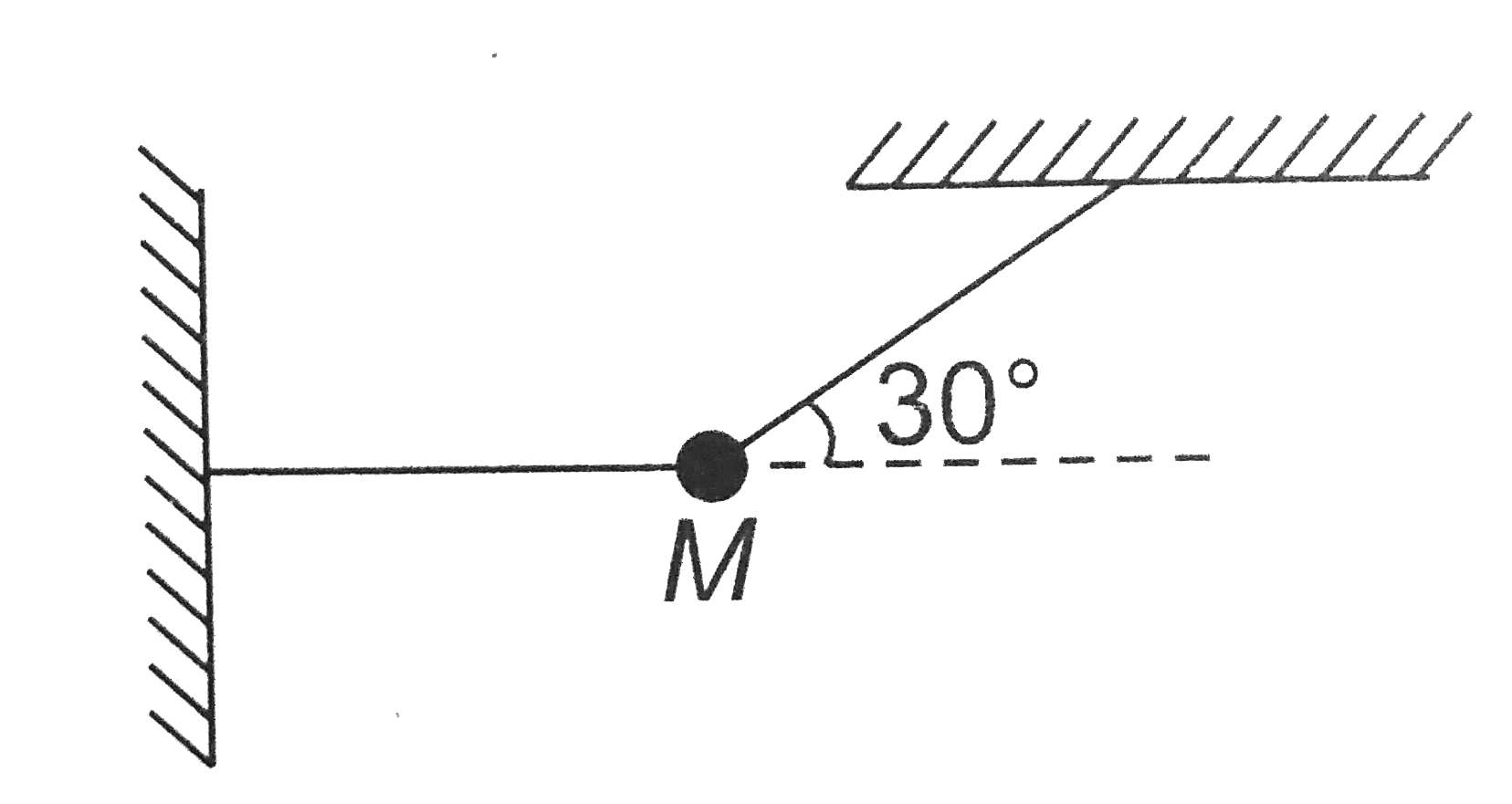
One end of a light string is fixed to the celling and the other end is tied to the wall. A body of mass 500 g is suspended from that string in such a way that the part of the string towards the wall remains horizontal and the portion towards the ceiling makes an angle of ${30}^{\circ }$ with the ceiling. Find the tension on the two parts of the string.

Explanation

Let the positive y-axis be vertically upwards and the x-axis be horizontal Fig. Let `T_(1)`= tension in the horizontal part of the string, `T_(2)` = tension in the other part of the string, W = weight of the suspended body= `500xx981 dyn`.
Sum of the components of the force along y-axis `=T_(2)sin30^(@)`-W
Sum of the components of the forces along x-axis
`T_(1)-T_(2)cos 30^(@)`
As the system is in equilibrium,
`T_(2) sin30^(@)-W = 0 " "cdots(1)`
`T_(1)-T_(2)cos 30^(@)=0 " "cdots (2)`
From (1),
`(1)/(2)T_(2)= W`
or, `T_(2)=`2W
`=2xx500xx981 dyn = 2xx(500xx981)/(10^(5))N= 9.81 N`
From (2),
`T_(1)=T_(2)cos 30^(@)= 9.81 xxcos 30^(@)=8.5 N`.