A body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
To find the tensions in the strings supporting a body of mass m suspended at angles α and β with the horizontal, we can follow these steps:
1. Identify Forces:
The body is in equilibrium, meaning the net force acting on it is zero. The forces acting on the body are:
- The weight of the body, W=mg (acting downwards).
- The tensions in the two strings, T1 and T2.
2. Resolve Tensions into Components:
- For string 1 (making angle α with the horizontal):
- Horizontal component: T1cosα
- Vertical component: T1sinα
- For string 2 (making angle β with the horizontal):
- Horizontal component: T2cosβ
- Vertical component: T2sinβ
3. Set Up Equilibrium Conditions:
- Since the body is in equilibrium, the sum of the forces in the horizontal direction must equal zero:
T1cosα=T2cosβ(1)
- The sum of the forces in the vertical direction must also equal zero:
T1sinα+T2sinβ=mg(2)
4. Express T2 in terms of T1:
From equation (1):
T2=T1cosαcosβ(3)
5. Substitute T2 into the Vertical Force Equation:
Substitute equation (3) into equation (2):
T1sinα+(T1cosαcosβ)sinβ=mg
6. Factor Out T1:
T1(sinα+cosαsinβcosβ)=mg
7. Simplify the Equation:
The term inside the parentheses can be simplified using the identity for sine:
sinα+cosαsinβcosβ=sinαcosβ+cosαsinβcosβ=sin(α+β)cosβ
Thus, we have:
T1sin(α+β)cosβ=mg
8. Solve for T1:
T1=mgcosβsin(α+β)(4)
9. Substitute T1 back to find T2:
Using equation (3):
T2=T1cosαcosβ=mgcosβcosαsin(α+β)(5)
Final Results:
- The tension in string 1:
T1=mgcosβsin(α+β)
- The tension in string 2:
T2=mgcosαsin(α+β)
The body is in equilibrium, meaning the net force acting on it is zero. The forces acting on the body are:
- The weight of the body, W=mg (acting downwards).
- The tensions in the two strings, T1 and T2.
- For string 1 (making angle α with the horizontal):
- Horizontal component: T1cosα
- Vertical component: T1sinα
- For string 2 (making angle β with the horizontal):
- Horizontal component: T2cosβ
- Vertical component: T2sinβ
- Since the body is in equilibrium, the sum of the forces in the horizontal direction must equal zero:
T1cosα=T2cosβ(1)
- The sum of the forces in the vertical direction must also equal zero:
T1sinα+T2sinβ=mg(2)
From equation (1):
T2=T1cosαcosβ(3)
Substitute equation (3) into equation (2):
T1sinα+(T1cosαcosβ)sinβ=mg
T1(sinα+cosαsinβcosβ)=mg
The term inside the parentheses can be simplified using the identity for sine:
sinα+cosαsinβcosβ=sinαcosβ+cosαsinβcosβ=sin(α+β)cosβ
Thus, we have:
T1sin(α+β)cosβ=mg
T1=mgcosβsin(α+β)(4)
Using equation (3):
T2=T1cosαcosβ=mgcosβcosαsin(α+β)(5)
- The tension in string 1:
T1=mgcosβsin(α+β)
- The tension in string 2:
T2=mgcosαsin(α+β)
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -114videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -29videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions64videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
Similar Questions
A body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 View Solution
View SolutionThe block of mass m is at rest. Find the tension in the string A .
 View Solution
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View SolutionA body of weight W is suspended by a string It is pulled aside with a horizontal force of 2W and held at rest. The tension in it is
View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.
 View Solution
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View SolutionA body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
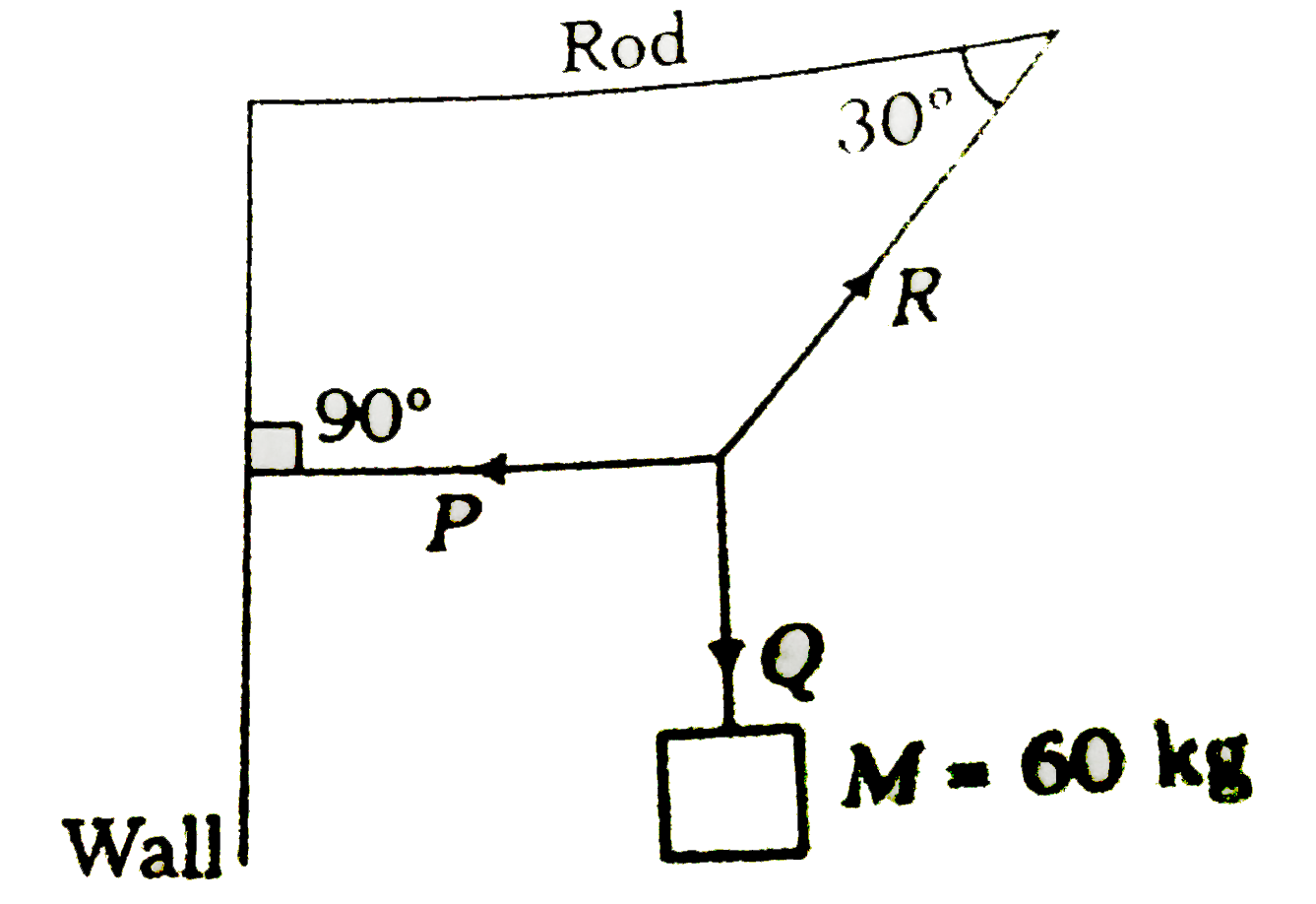 View Solution
View SolutionA body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
 View Solution
View Solution

