Find the moment of inertia of a sphere about a tangent to the sphere. Given the moment of inertia of the sphere about any of its diameters to be 2MR25 , where M is the mass of the sphere and R is the radius of the sphere.
Text Solution
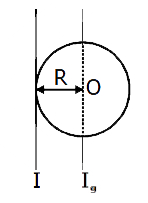
The centre of mass (cm) of the sphere is on its diameter AB Fig .Icm=25MR2
According to the parallel-axes theorem the moment of inertia of the sphere about the tangent CD,
I=Icm+MR2=25MR2+MR2=75MR2

|
Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXERCISE (Multiple Choice Questions )
9 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXERCISE ( Based on Torque )
2 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Section Related Question
2 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2If temperature increases, the moment of inertia of a solid sphere about its diameter
AincreasesBdecreasesCremains unchangedDbecomes negativeWith the increase in temperate, moment of inertia of a solid sphere about the diameter.
AdecreasesBincreasesCdoes not changeDnone of these
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionThe moment of inertia of a soild sphere about a tangent is 53mr2. What would be its moment of inertia about its diameter.
View SolutionThe moment of inertia of a sphere is 40 kg-m2 about its diametric axis. Determine the moment of inertia about any tangent.
View SolutionFind the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.
View SolutionThe moment of inertia of a sphere is 20 kg-m2 about the diameter. The moment of inertia about any tangent is
View Solution
