A solid sphere of mass m and radius R rolls down from the top of a table. With how much angular speed will it touch the ground?
At position II the resultant of mg cos θ and n supplies the necessary centripetal force to roll on i.e.,
mω2R=mgcosθ−n
[ ω = angular speed of the sphere ]
When n = 0, the sphere will not be in contact more with the table. Then mω2R=mgcosθ or,cosθ=ω2Rg
The centre of mass of the sphere is lowered down by R (1-cos θ).
Let I be the moment of inertia of the sphere about the tan gent at the contact point between the table and the sphere. From the conservation law of mechanical energy,
mg.R(1−cosθ)=12×Iω2=710mR2ω2[∵I=75mR2]
∴ mgR(1−ω2Rg)=710mR2ω2
or, mgR−mω2R2=710mR2ω2
∴ ω=√10g17R
Considering a free fall of the sphere as no torque acts on it this angular speed remains unaltered. It means that the sphere touches the ground with an angular speed √10g17R.

Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXERCISE (Multiple Choice Questions )
9 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXERCISE ( Based on Torque )
2 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Section Related Question
2 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
A12R√ghB2R√ghC2R√gh3D2R√gh2A solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
A√34ghB√43ghC√4ghD√2ghThree solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
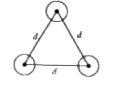 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA ring,solid sphere and a disc are rolling down from the top of the same height, then the sequence to reach on the surface is
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
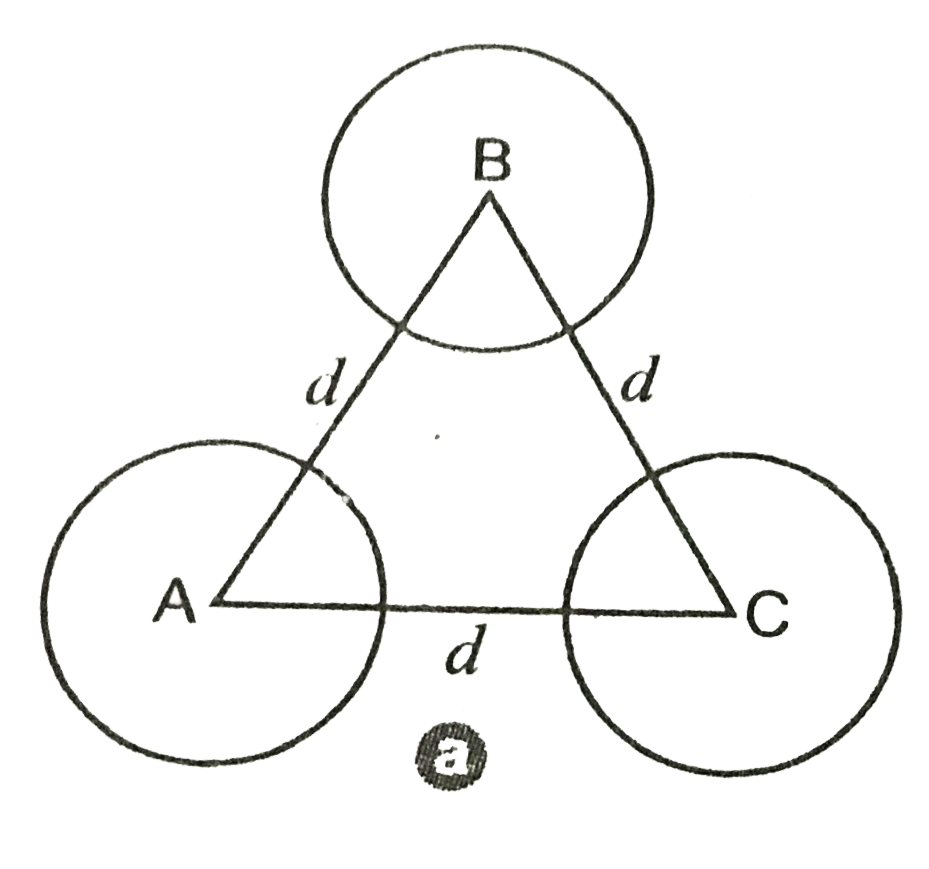
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?

View SolutionThe ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is
View Solution
