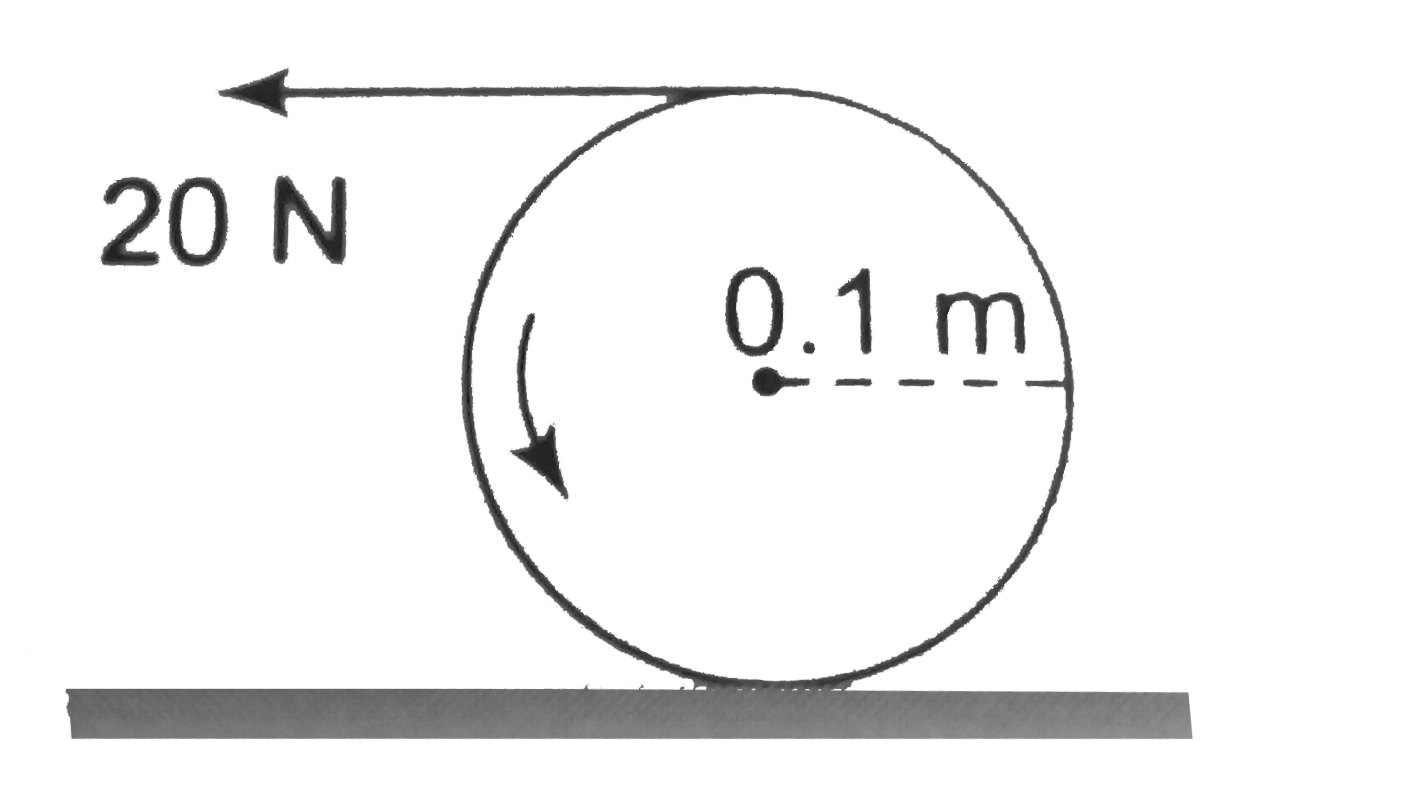
A rope is wound on a circular disc of moment of inertia 0.1 kg . m2. A tangential force of 20 N on the rope rotates the disc about its axis. If the radius of the wheel is 0.1 m, calculate its acceleration. Now a mass of 2 kg is suspended at the lower end of the rope. What will be the angular acceleration? g = 10 m.s−2
The correct Answer is:20 rad.s−2,16.7rad.s−2
Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Hots Numerical Problems ( Based on Torque )
2 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Hots Numerical Problems ( Miscellaneous )
7 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Problem Set - II (Miscellaneous )
3 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
A rope is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ?
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
 .
.
View Solution
Knowledge Check
A mass of 10 kg is suspended from a rope wound on a wheel of diameter 40 cm. The torque about the axis of rotation is
A39.2 N mB19.6 N mC4 N mD2 N mA disc of mass 2 kg and diameter 40 cm is free to rotate about an axis passing through its centre and perpendicular to its plane. If a force of 50 N is applied to the disc tangentially Its angular acceleration will be
A100rad/s2B25rad/s2C250rad/s2D500rad/s2A wheel whose radius is R and moment of inertia about its own axis is I, rotates freely about its own axis. A rope is wrapped on the wheel. A body of mass m is suspended from the free end of the rope. The body is released from rest. The velocity of the body after falling a distance h would be:
A(mghI)1/2B(2mghm+I)1/2C(2mghm+I/r2)1/2D(m+I2mgh)1/2
The moment of inertia of a circular disc about its diameter is 500 kg m2. If its radius is 2 m, than its radius of gyration is
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
 .
.
View SolutionThe moment of inertia of a solid flywheel about its axis is 0.1kg−m2.A tangential force of 2 kg-wt. is applied round the circumference of the flywheel with the help of a string and mass arrangement as shown in the figure. If the radius of the wheel is 0.1 m, find the acceleration (in rad/sec2) of the mass :
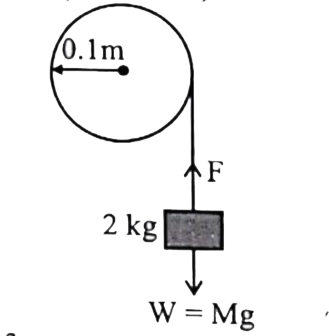
View SolutionIf the radius of gyration of a solid disc of mass 10 kg about an axis is 0.40 m, then the moment of inertia of the disc about that axis is
View SolutionAn object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
View Solution
