Statement I : Moment of inertia of uniform disc and solid cylinder of equal mass and radius about an axis passing through the centre and perpendicular to the plane will be same.
Statement II : Moment of inertia depends upon distribution of mass from the axis of rotation, i.e., perpendicular distance from the axis.Solution in Bengali
Statement I is true, statement II is true , statement II is a correct explanation for statement I.
Statement I is true, statement II is true , statement II is not a correct explanation for statement I.
Statement I is true, statement II is false.
Statement I is false, statement II is true.
The correct Answer is:A
Step by step video, text & image solution for Statement I : Moment of inertia of uniform disc and solid cylinder of equal mass and radius about an axis passing through the centre and perpendicular to the plane will be same. Statement II : Moment of inertia depends upon distribution of mass from the axis of rotation, i.e., perpendicular distance from the axis. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - ENTRANCE CORNER ( Multiple correct answers type )4videos
ROTATION OF RIGID BODIES
- BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - ENTRANCE CORNER ( Comprehension type )6videos
ROTATION OF RIGID BODIES
- BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Hots Numerical Problems ( Miscellaneous )7videos
ROTATION OF RIGID BODIES
- BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II20videos
QUESTION PAPERS OF WBCHSE -2018
- BOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER16videos
SIMPLE HARMONIC MOTION
Similar Questions
In which of the following cases is the angular momentum conserved ?
01:56View SolutionTwo discs A and B are mounted co-axially on a vertical axie. The discs have moments of inertia I and 2I , respectively, about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1. Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the discs rotate in the clockwise direction.
The ratio x1x2 is02:25View SolutionThe moment of inertia of a disc is 5×10(−4)kg.m2. It is rotating freely about a vertical axis passing through its centre at a speed of 40 rpm. A piece of wax of mass 20 g is attached at a distance of 8 cm from its centre. Calculate its new speed.
06:23View Solutionwhat are the sighificant figures in the result of addition of 9.8 and 15.298 ?
02:12View SolutionExplain the relation in phase between displacement velocity and acceleration in SHM, graphically as well as theoretically.
05:34View SolutionA Moment of inertial of uniform disc and solid cylinder of equal mass and equal radius about an axis passing through centre and perpendicluar to plane will to same. Moment of inertia depends upon distribution of mass from the axis of rotation i.e., perpendicular distance from the axis.
02:44View SolutionStatement-1 : Moment of inertia of a particle is same, whatever be the axis of rotation. Statement-2 : Moment of inertia depends on mass and perpendicular distance of the particle from its axis of rotation.
04:26View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
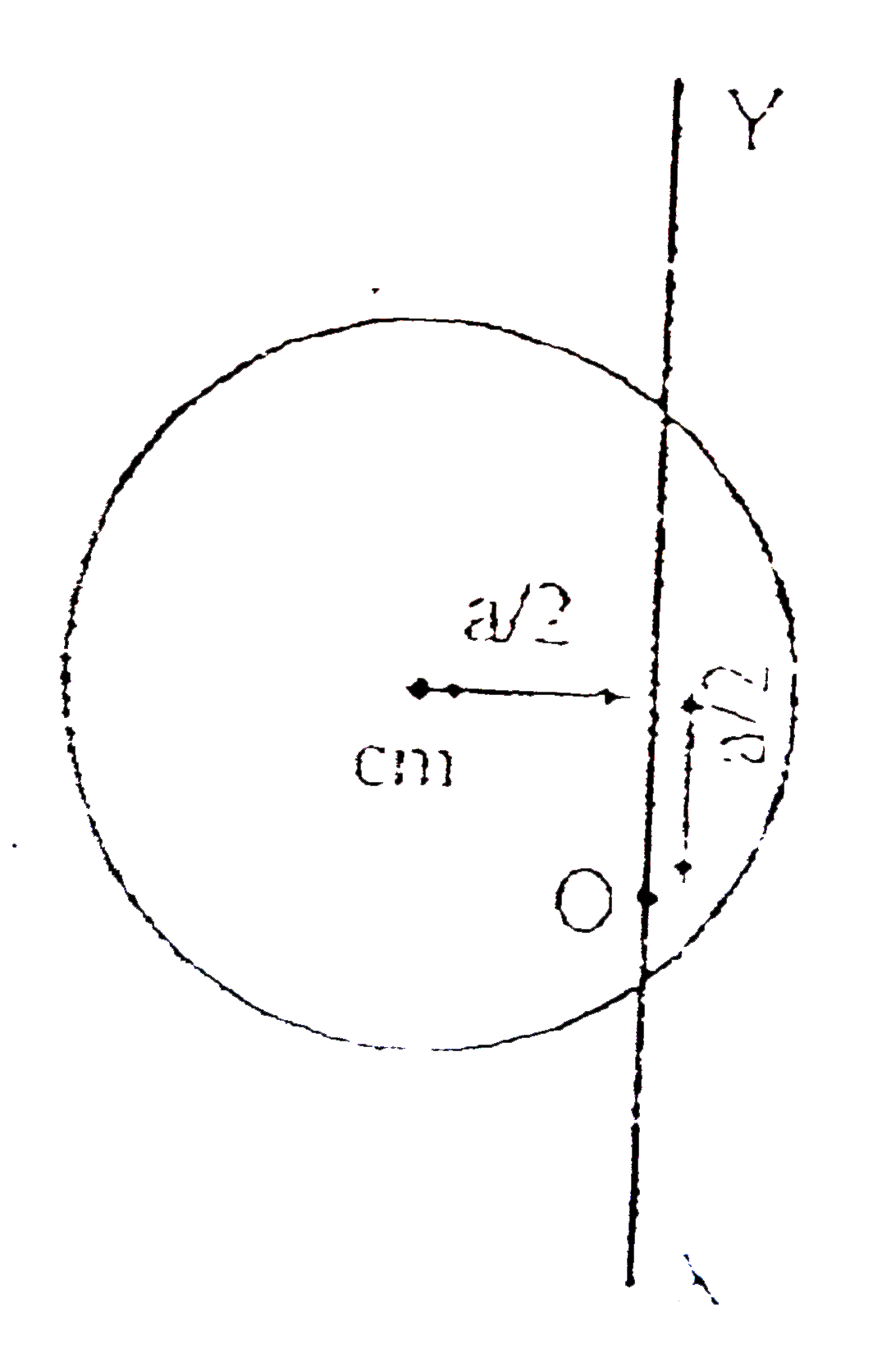 View Solution
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
02:51View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
07:28View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
03:46View SolutionThe moment of inertia of a circular disc of mass m and radius r about an perpendicular axis passing through its centre is
04:27View Solution1kg द्रव्यमान तथा 2m त्रिज्या की वृत्तीय चकती के तल के लम्बवत्, द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण 2kgm2 है। चकती के सतह से गुजरने वाले अक्ष के समानान्तर जड़त्व आघूर्ण होगा (दिये गये चित्रानुसार)
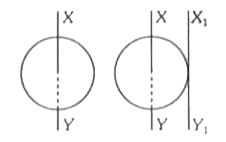 04:37View Solution
04:37View SolutionA solid sphere of mass M and radius R having moment of inertia about an axis passing through the centre of mass as I, is recast into a disc of thickness I, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains I. Then, radius of the disc will be
View Solution

