Calculate the moment of inertia of a ring about an axis passing through centre of the ring and perpendicular to the plane of the ring. Solution in Bengali
Let M be the mass of the ring with radius r and centre O. Length of the ring = 2 πr
Mass per unit length of the ring = m2πr
Now, mass of length element dx=m2πr.dx
Moment of inertia of this element about the axis
=(m2πrdx)r2=mr2π.dx
Hence moment of inertia of the entire ring about the axis,
I=∫2πr0mr2πdx=mr2π∫2πr0dx
=mr2π(2πr−0)=mr2

Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (NEET )8videos
ROTATION OF RIGID BODIES
- BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II20videos
QUESTION PAPERS OF WBCHSE -2018
- BOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER16videos
SIMPLE HARMONIC MOTION
Similar Questions
From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
02:11View Solutionwhat are the sighificant figures in the result of addition of 9.8 and 15.298 ?
01:25View SolutionExplain the relation in phase between displacement velocity and acceleration in SHM, graphically as well as theoretically.
02:43View SolutionCalculate the moment of inertia of a ring having mass M , radius R and having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
02:37View SolutionFrom a complete ring of mass M and radius R , a 30^@ sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ,
03:07View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
03:18View SolutionI is moment of inertia of a thin circular ring about an axis perpendicular to the plane of ring and passing through its centre. The same ring is folded into 2 turns coil. The moment of inertia of circular coil about an axis perpendicular to the plane of coil and passing through its centre is
02:15View SolutionThe moment of inertia of ring about an axis passing through its diameter is I . Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionA ring of mass 10 kg and diameter 0.4m is rotated about an axis passing through its centre and perpendicular to its plane moment of inertia of the ring is
02:42View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
02:30View SolutionWhat is the ratio of the moments of inertia of two rings radii r and nr about an axis perpendicular to their plane and passing through their centres?
03:47View SolutionFind the moment of inertia of ring about an axis passing through the centre and perpendicular to its plane.
02:30View SolutionThe moment of inertia of ring about an axis passing through its diameter is I . Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
02:28View SolutionCalculate the moment of inertia of a ring about in axis passing through centre and perpendicular to its plane.
01:37View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
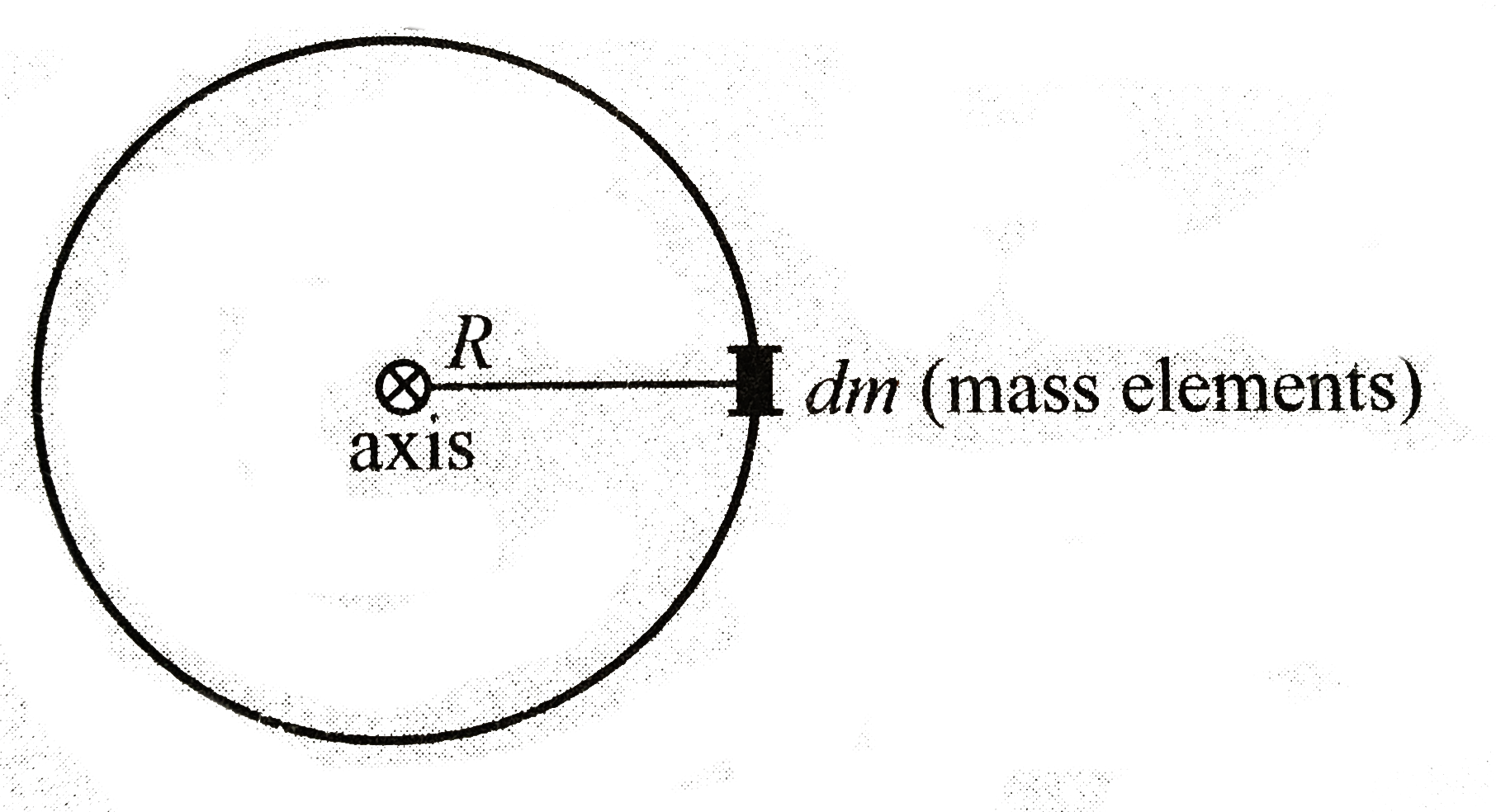 02:07View Solution
02:07View Solution

