A rocket is projected vertically upwards from the surface of the earth (radius =R) with a velocity v. To what height will the rocket rise ?(Neglect air friction)
h=R2gRv2−1
h=R2gRv2+1
h=R(2gRv2−1)
h=R(2gRv2+1)
The correct Answer is:A
Topper's Solved these Questions
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - EXERCISE (Very Short Answer Type Questions)
67 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - EXERCISE (Short Answer Type Questions-I)
12 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
41 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - CBSE SCANNER
24 Videos
- ONE - DIMENSIONAL MOTION BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - CBSE SCANNER
19 Videos
Similar Questions
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
View SolutionAn object is projected vertically upward from the surface of the earth of mass M with a velocity such that the maximum height reached is eight times the radius R of the earth. Calculate:
(i) the initial speed of projection
(ii) the speed at half the maximum height.
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A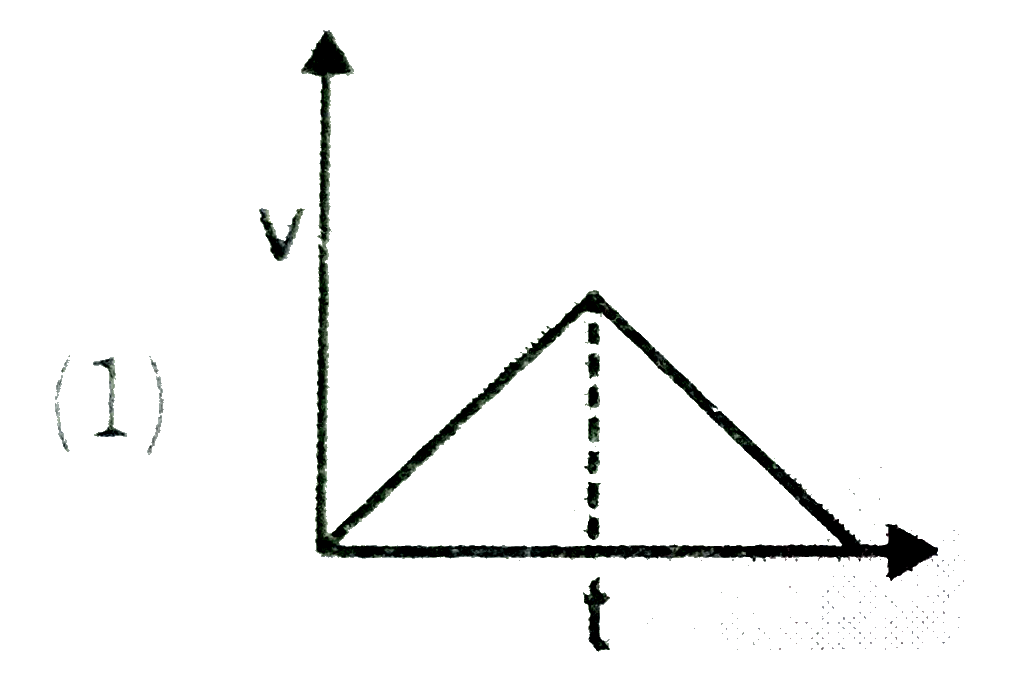 B
B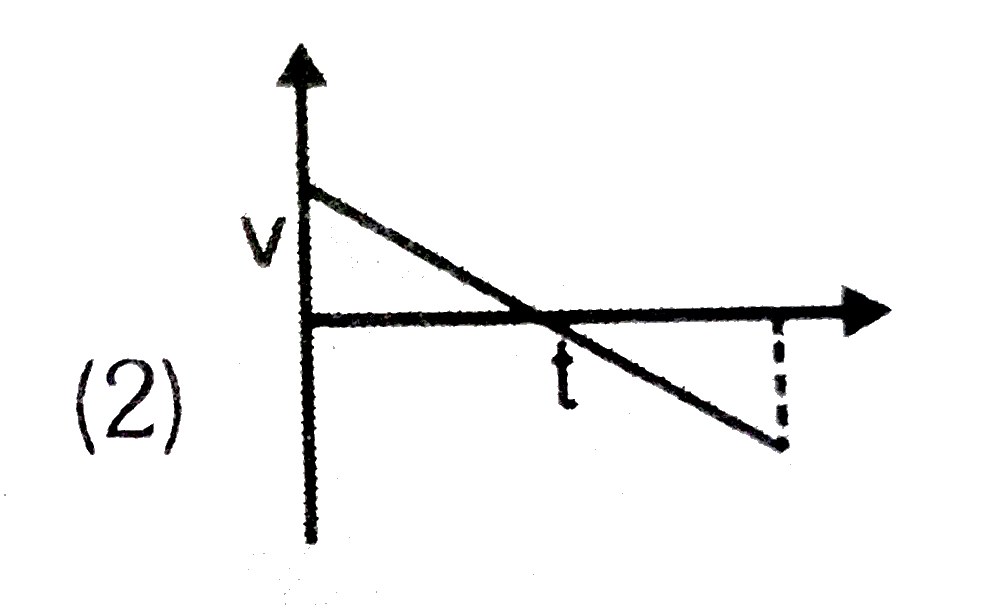 C
C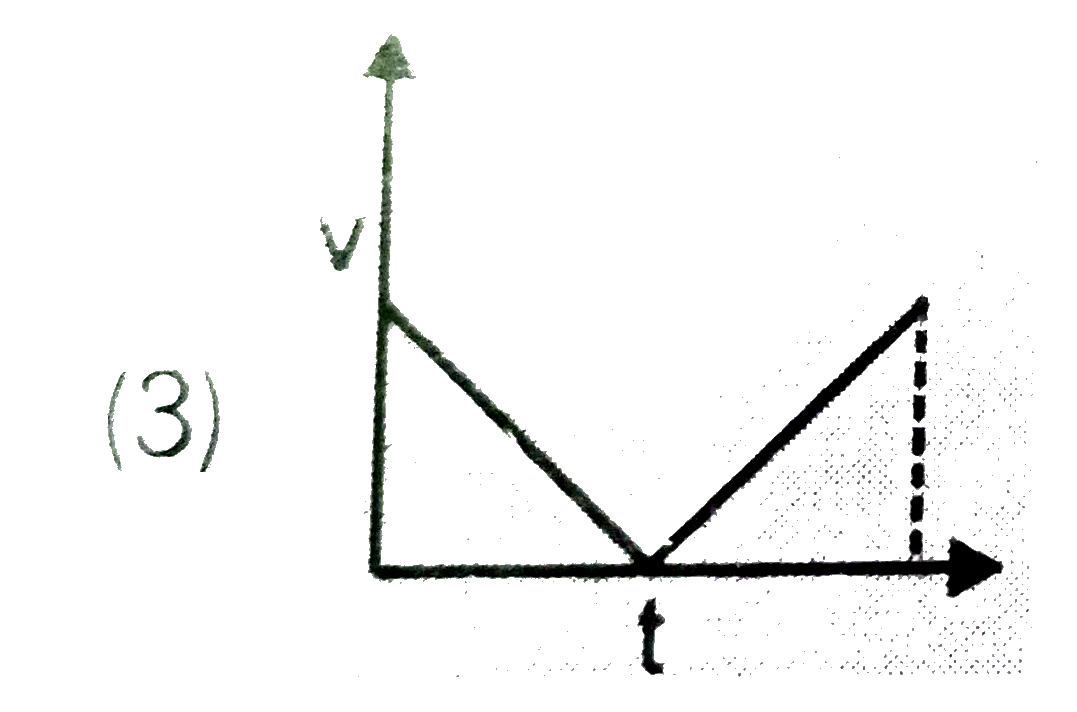 D
D
A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
AR/2BR/3CR/5DR/4A rocket is launched vertically from the surface of the earth with an initial velocity v. How far above the surface of earth will it go? Neglect the air resistance. (where R is the radius of the earth )
AR(2gRv2−1)−1/2BR(2gRv2−1)CR(2gRv2−1)−1DR(2gRv2−1)2
A body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionA particle is projected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
View SolutionA projectile is fired vertically upwards from the surface of the earth with a velocity Kve, where ve is the escape velocity and K<1.If R is the radius of the earth, the maximum height to which it will rise measured from the centre of the earth will be (neglect air resistance)
View Solution
