A uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal. Determine θ.
The correct Answer is:sin−1(12√ρ0ρ)
Topper's Solved these Questions
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - ENTRANCE CORNER (ASSERTION-REASON TYPE)
7 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - MULTIPLE CORRECT ANSWERS TYPE
4 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - PROBLEM SET - II
32 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - CBSE SCANNER
7 Videos
- KINETIC THEORY OF GASESBOOK - CHHAYA PUBLICATIONCHAPTER - KINETIC THEORY OF GASESEXERCISE - CBSE Scanner
9 Videos
Similar Questions
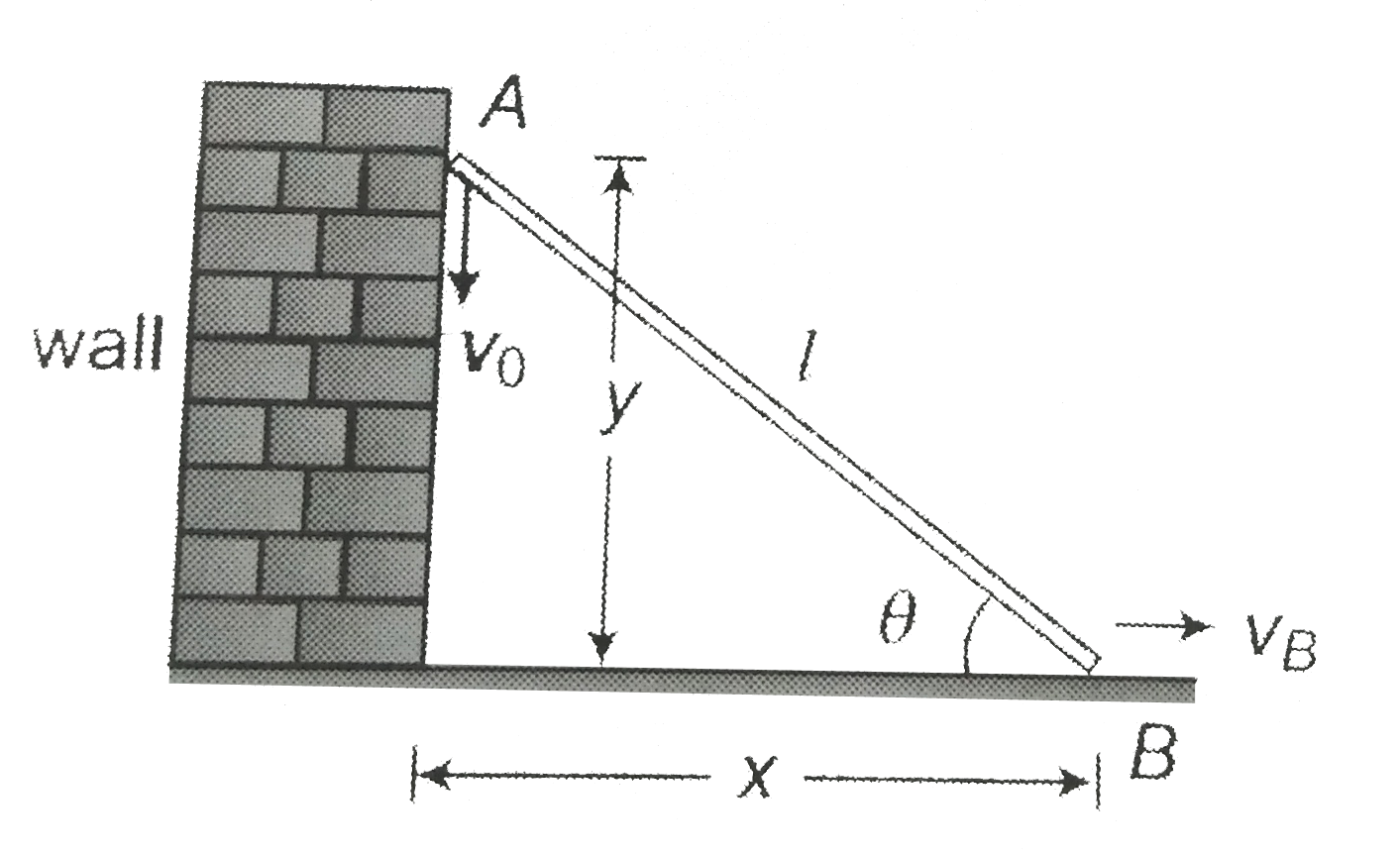
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View Solution
Knowledge Check

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρaA liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
Asin−1(√ρ0ρ)Bsin−1(n√ρ0ρ)Csin−1(1n√ρ0ρ)Dsin−1(1n√ρρ0)A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
Asin−1(√ρ0ρ)Bsin−1(n√ρ0ρ)Csin−1(1n√ρ0ρ)Dsin−1(1n√ρρ0)
A sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View Solution
