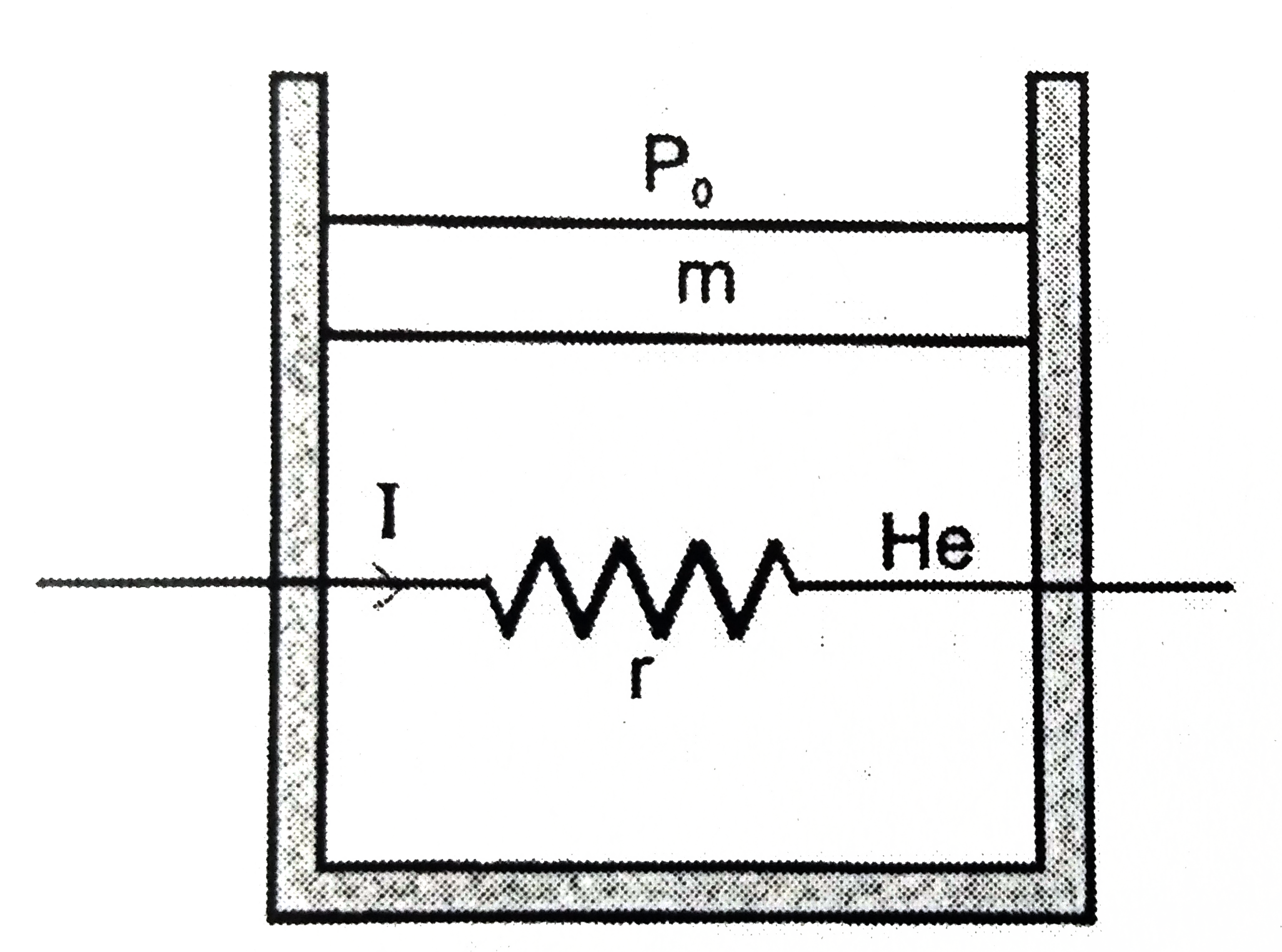
A heating element of resistance r is fitted inside an adiabatic cylinder which carries a frictionless piston of mass m and cross section A as shown in diagram gas. The current flows through the element such that the temperature rises with time t as ΔT=α+12βt2(αandβareconstant), while pressure remains constant. the atmospheric pressure above the piston is P0. Then

the rate of increase in internal energy is 52R(α+βt)
the current flowing in the element is √52rR(α+βt)
the piston moves upwards with constant acceleration
the piston moves upwards with constant speed
The correct Answer is:A, C
Increase in internal energy,
ΔU=nCvΔT=1×52R×(αt+12βt2)
=52R(αt+12βt2)
Rate of increase in internal energy,
d(ΔU)dt=52R(α+βt)
According to Charles. law, ΔV∝ΔT [when pressure constant]
∴ΔV=C(αt+12βt2) [C = constant]
So, displacement of the piston,
Δx=ΔVA=C.(αt+12βt2)[C.=CA = constant]
Hence, the displacement of the piston obeys the equation of motion of a particle in constant acceleration.
Topper's Solved these Questions
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - Examination Archive with solution (JEE Main)
6 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - Examination Archive with solution (AIPMT)
6 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - Examination Archive with solution (WBCHSE)
25 Videos
- EXPANSION OF SOLIDS AND LIQUIDSBOOK - CHHAYA PUBLICATIONCHAPTER - EXPANSION OF SOLIDS AND LIQUIDSEXERCISE - CBSE SCANNER
2 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - CBSE SCANNER
7 Videos
Similar Questions
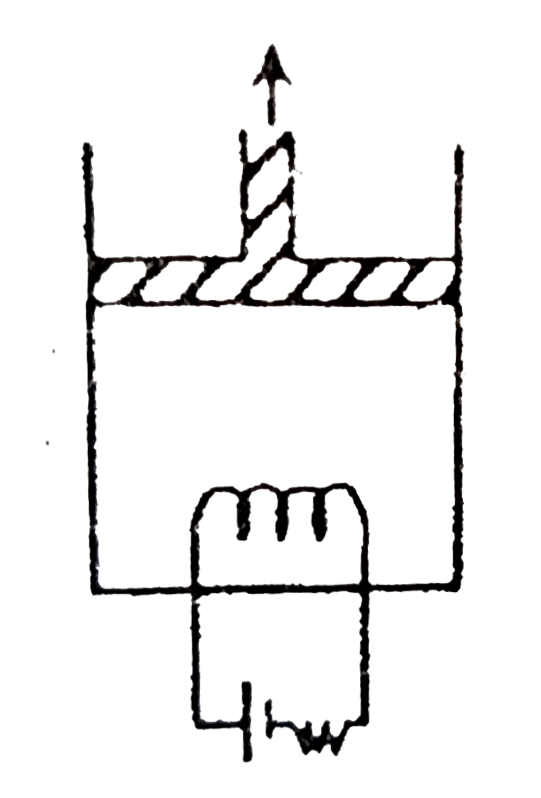
A resistance coil of resistance r connected to an external battery, is placed inside an adiabatic cylinder fitted with a frictionless platon of mass m and same area A. Initially cylinder contains one mole of ideal gas he. A current through the coil such that temperature of gas varies as T=T0+at+bt2, keeping pressure constant with time t. Atosphere pressure above piston is P0. Find
(a) Current l flowing through the coil as function of time and
(b) Speed of piston as function of time.
View SolutionA resistance coil, connected to an external battery is placed inside an adiabatic cylinder filled with frictionless piston of mass m and containing an ideal gas. A current i flows through the coil, which has resistance R. The speed with which the piston must move in order to keep the temperature of the gas constant will be
View Solution
Knowledge Check
A heating element of piston resistance r is fitted inside an adiabatic cylinder which carries a frictionless piston of mass m and crosssection A as shown in diagram. The cylinder contains one mole of an ideal diatomic gas. The current flows through the element such that the temperature rises with time t as ΔT=alpaht+12βt2? (α and β are constants), while pressure remains constant. The atmospheric pressure above the piston is P0. Then
 Athe rate of increase in internal energy is 52R(α+βt)Bthe current flowing in the element is √52rR(α+βt)Cthe piston moves upwards with constant acceleration,Dthe piston moves upwards with constant speed.
Athe rate of increase in internal energy is 52R(α+βt)Bthe current flowing in the element is √52rR(α+βt)Cthe piston moves upwards with constant acceleration,Dthe piston moves upwards with constant speed.A resistance coil, connected to an external battery is placed inside an adiabatic cylinder filled with frictionless piston of mass m and containing an ideal gas. A current i flows through the coil, which has resistance R. The speed with which the piston must move in order to keep the temperature of the gas constant will be
 Ai2R/mgBiR/mgC0DData is insufficient.
Ai2R/mgBiR/mgC0DData is insufficient.The charge flowing through a resistance R varies with time tasQ=at−bt2. The total heat produced in R is
Aα2R2βBα3R6βCα3RβDNone
The temperature (T) of one mole of an ideal gas varies with its volume (V) as T=−αV3+βV2, where αandβ are positive constants. The maximum pressure of gas during this process is
View SolutionPressure p, volume V and temperature T for a certain gas are related by
p=αT−βT2V
where, α and β are constants. Find the work done by the gas if the temperature changes from T1 to T2 while the pressure remains the constant.
View SolutionPressure p, volume V and temperature T for a certain gas are related by
p=αT−βT2V
where, α and β are constants. Find the work done by the gas if the temperature changes from T1 to T2 while the pressure remains the constant.
View SolutionThe temperature (T) of one mole of an ideal gas varies with its volume (V) as T=−αV3+βV2, where αandβ are positive constants. The maximum pressure of gas during this process is
View SolutionA current through a wire depends on time as i=α0t+βt2 where α0=20A/s and β=8As−2 . Find the charge crossed through a section of the wire in 15 s.
View Solution
