One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure.

The change in internal energy of the gas during the transition is
20 KJ
−20KJ
20 J
−12KJ
The correct Answer is:B
For an ideal diatomic gas, Cv=52R
So, change in internal energy,
ΔU=Cv(TB−TA)=52R(pBVBR−pAVAR)
=52(pBVB−pAVA)
=52{(2×103)×−(5×103)×4}
=−52×8×103=−20×103J=−20KJ.
Topper's Solved these Questions
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - Examination Archive with solution (NEET)
7 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - Examination Archive with solution (JEE Main)
6 Videos
- EXPANSION OF SOLIDS AND LIQUIDSBOOK - CHHAYA PUBLICATIONCHAPTER - EXPANSION OF SOLIDS AND LIQUIDSEXERCISE - CBSE SCANNER
2 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - CBSE SCANNER
7 Videos
Similar Questions
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
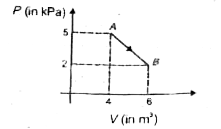
The change to internal energy of the gas during the transition is
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure

The change to internal energy of the gas during the transition is
View Solution
Knowledge Check
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
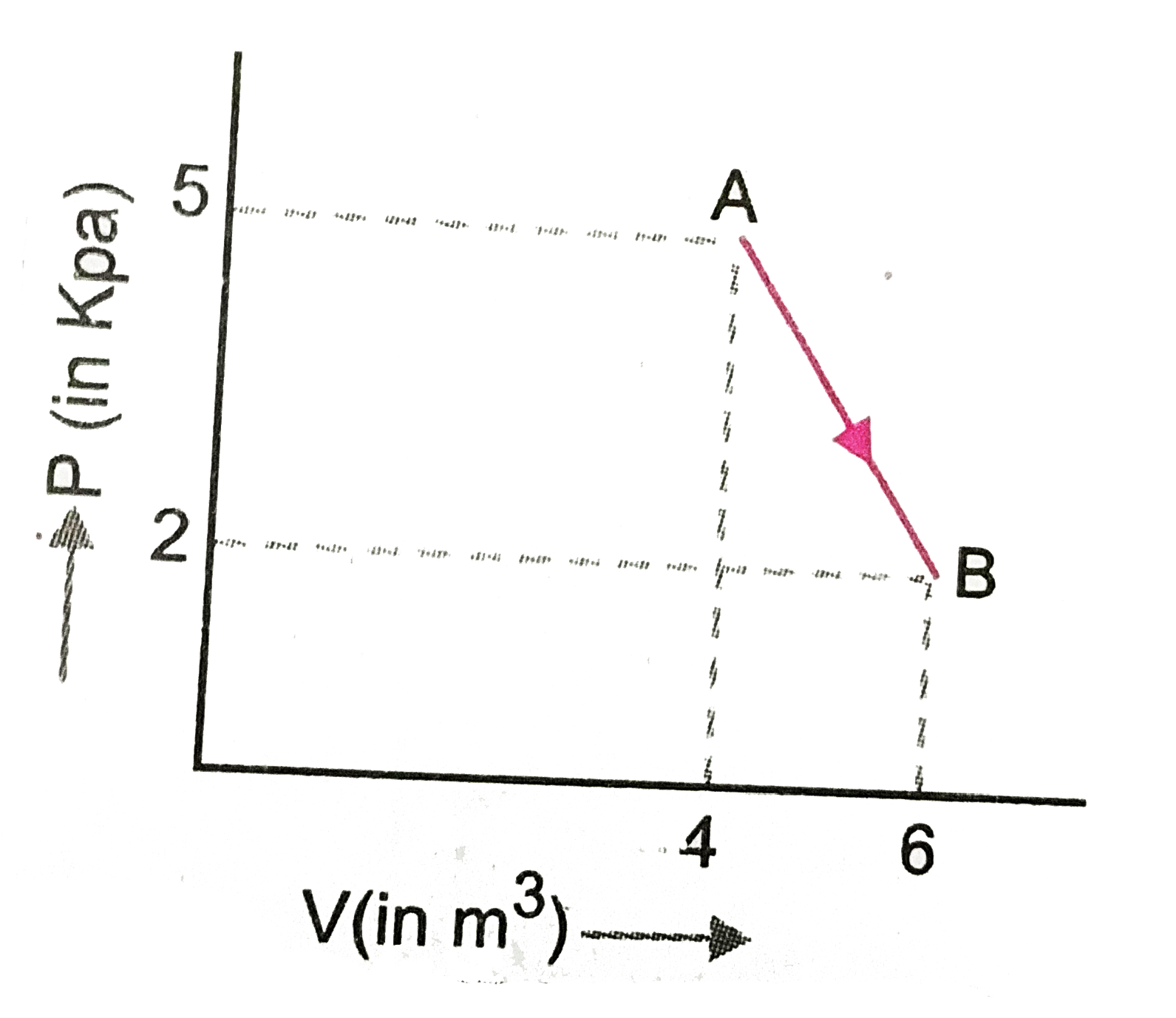 A−20KJB20KJC−12KJD20KJ
A−20KJB20KJC−12KJD20KJOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
 A−20KJB20 JC−12KJD20 KJ
A−20KJB20 JC−12KJD20 KJA mono-atomic gas is taken along path AB as shown. Calculate change in internal energy of the gas.
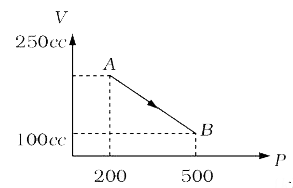 A279.8JB341JC241JDzero
A279.8JB341JC241JDzero
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)

View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)

View Solution0.5 moles of an ideal monoatomic gas undergoes a thermodynamic process from A to B as shown in figure. The change in internal energy of the gas during the process from A to B is
View SolutionA mono-atomic gas is taken along path AB as shown. Calculate change in internal energy of the gas.

View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure. Then the change in the energy in expanding the gas from a to c along the path abc is:

View Solution
