0.5 moles of an ideal monoatomic gas undergoes a thermodynamic process from A to B as shown in figure. The change in internal energy of the gas during the process from A to B is
-7 kJ
– 21 kJ
- 28 kJ
- 42 kJ
To find the change in internal energy (ΔU) of the ideal monoatomic gas during the process from A to B, we can follow these steps:
1. Identify the Formula for Change in Internal Energy:
The change in internal energy for an ideal monoatomic gas is given by the formula:
ΔU=32nRΔT
where n is the number of moles, R is the universal gas constant, and ΔT is the change in temperature.
2. Relate Temperature Change to Pressure and Volume:
We can express ΔT in terms of pressure and volume using the ideal gas law:
PV=nRT⟹T=PVnR
Therefore, the change in temperature can be expressed as:
ΔT=P2V2nR−P1V1nR
Simplifying this, we have:
ΔT=1nR(P2V2−P1V1)
3. Substituting Values:
From the problem, we have:
- n=0.5 moles
- The pressure at point A (P1) = 8×103 Pa
- The volume at point A (V1) = 8 m³
- The pressure at point B (P2) = 3×103 Pa
- The volume at point B (V2) = 12 m³
Now substituting these values into the equation for ΔT:
ΔT=10.5×R((3×103)(12)−(8×103)(8))
4. Calculate P2V2−P1V1:
Calculate P2V2 and P1V1:
P2V2=3×103×12=36×103
P1V1=8×103×8=64×103
Therefore,
P2V2−P1V1=36×103−64×103=−28×103
5. Substituting Back to Find ΔU:
Now substituting back into the equation for ΔU:
ΔU=32×0.5×R×−28×1030.5×R
Simplifying this gives:
ΔU=32×−28×103=−42×103 J=−42 kJ
6. Final Result:
Therefore, the change in internal energy of the gas during the process from A to B is:
ΔU=−42 kJ
The change in internal energy for an ideal monoatomic gas is given by the formula:
ΔU=32nRΔT
where n is the number of moles, R is the universal gas constant, and ΔT is the change in temperature.
We can express ΔT in terms of pressure and volume using the ideal gas law:
PV=nRT⟹T=PVnR
Therefore, the change in temperature can be expressed as:
ΔT=P2V2nR−P1V1nR
Simplifying this, we have:
ΔT=1nR(P2V2−P1V1)
From the problem, we have:
- n=0.5 moles
- The pressure at point A (P1) = 8×103 Pa
- The volume at point A (V1) = 8 m³
- The pressure at point B (P2) = 3×103 Pa
- The volume at point B (V2) = 12 m³
ΔT=10.5×R((3×103)(12)−(8×103)(8))
Calculate P2V2 and P1V1:
P2V2=3×103×12=36×103
P1V1=8×103×8=64×103
Therefore,
P2V2−P1V1=36×103−64×103=−28×103
Now substituting back into the equation for ΔU:
ΔU=32×0.5×R×−28×1030.5×R
Simplifying this gives:
ΔU=32×−28×103=−42×103 J=−42 kJ
Therefore, the change in internal energy of the gas during the process from A to B is:
ΔU=−42 kJ
Topper's Solved these Questions
Similar Questions
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
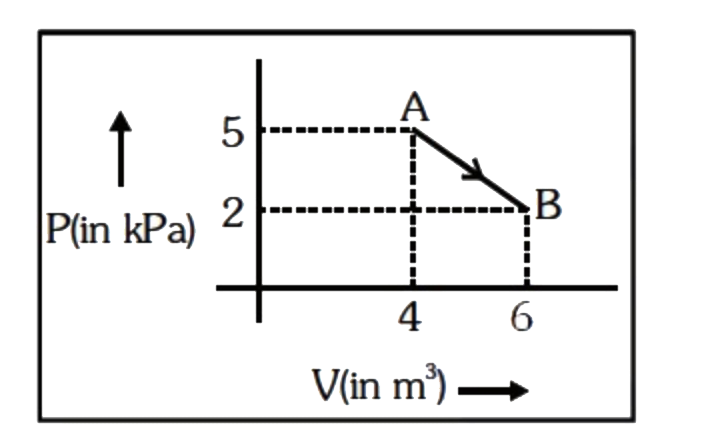
The change in internal energy of the gas during the transition is :
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
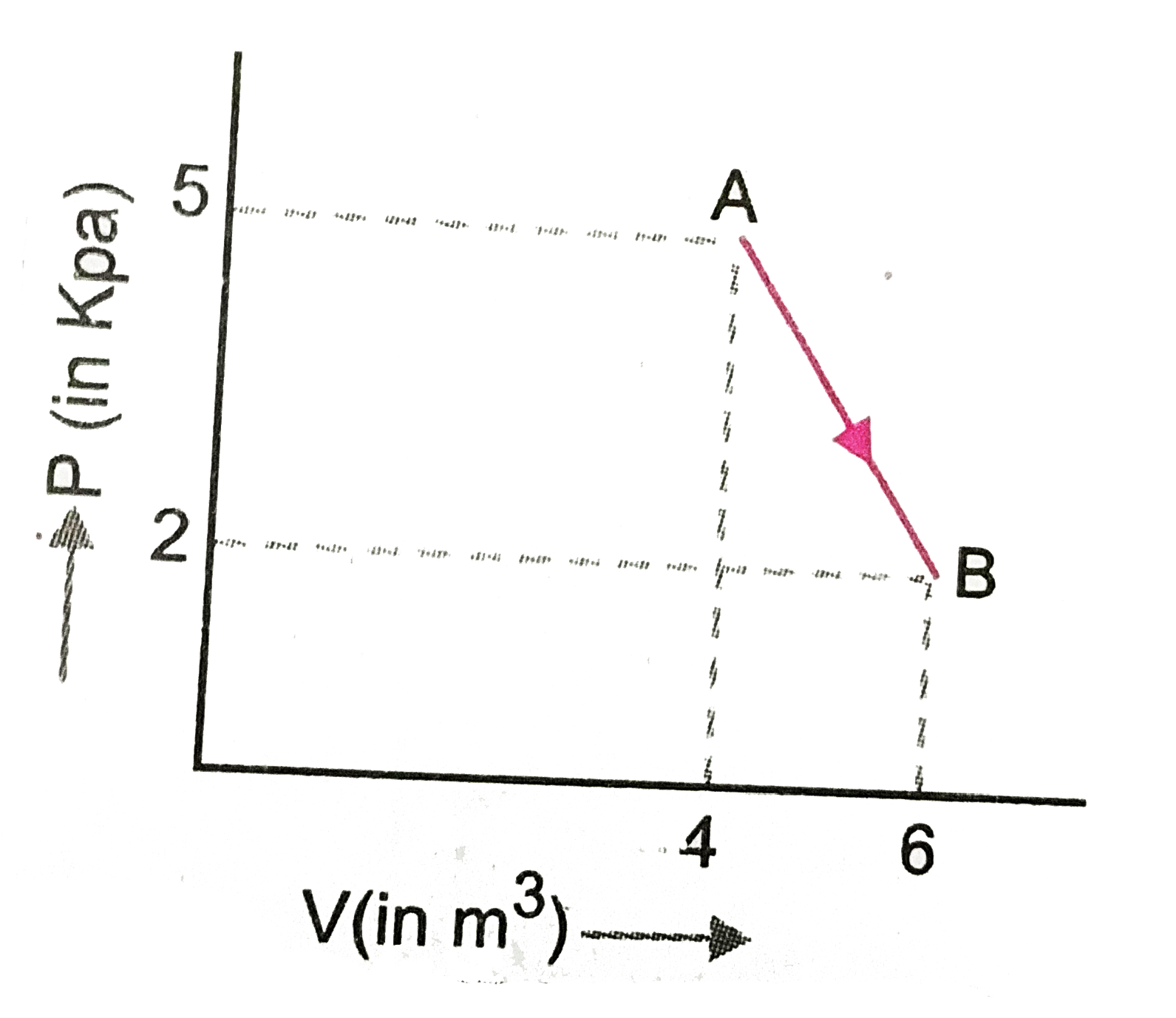
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)

View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
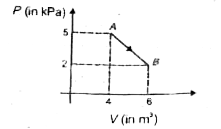
The change to internal energy of the gas during the transition is
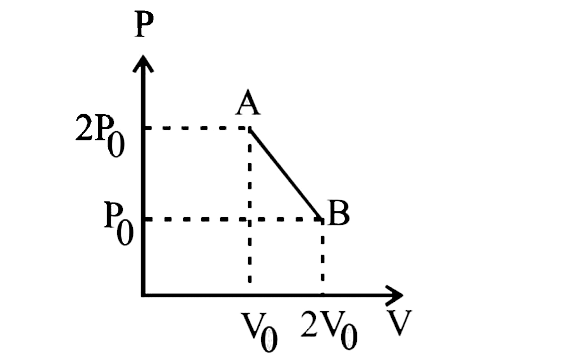
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
View SolutionAn ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id
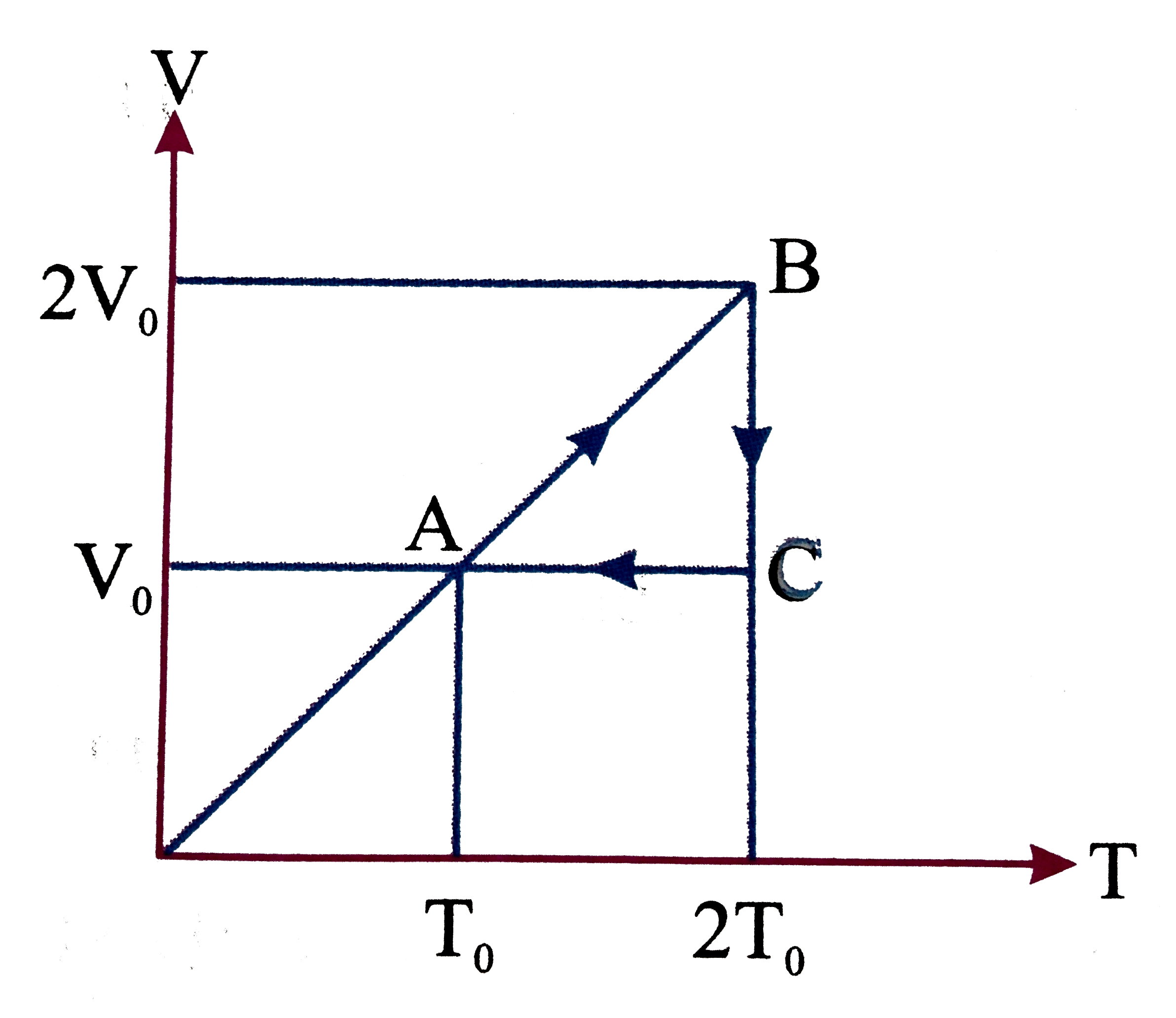
View SolutionOne mole of monoatomic ideal gas undergoes a process ABC as shown in figure. The maximum temperature of the gas during the process ABC is in the form xPVR . Find x .
_E01_281_Q01.png)
View SolutionChange in internal energy in an isothermal process for ideal gas is
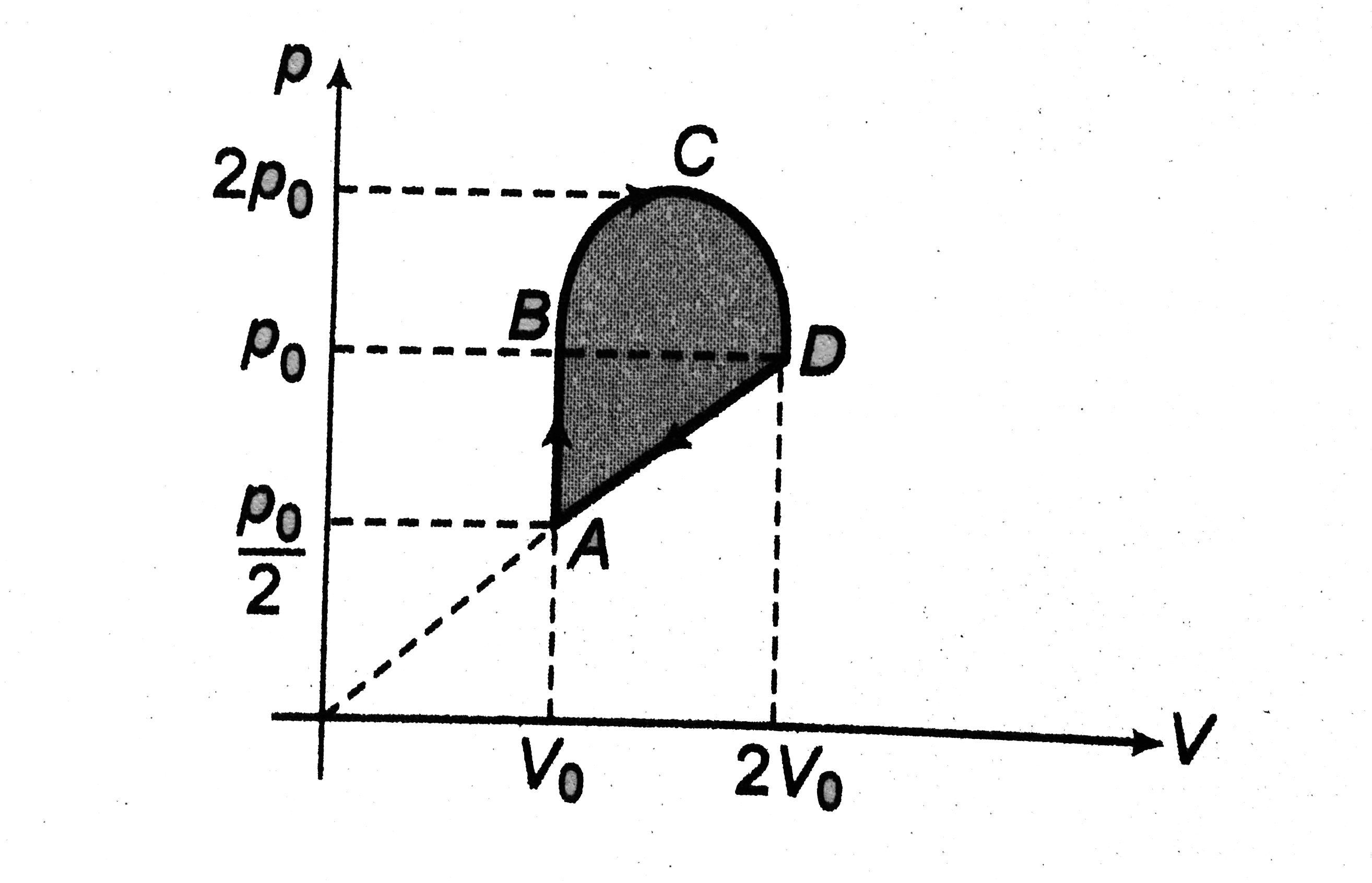
View SolutionTwo moles of a monatomic ideal gas undergo a cyclic process ABCDA as shown in figure. BCD is a semicircle. Find the efficiency of the cycle.
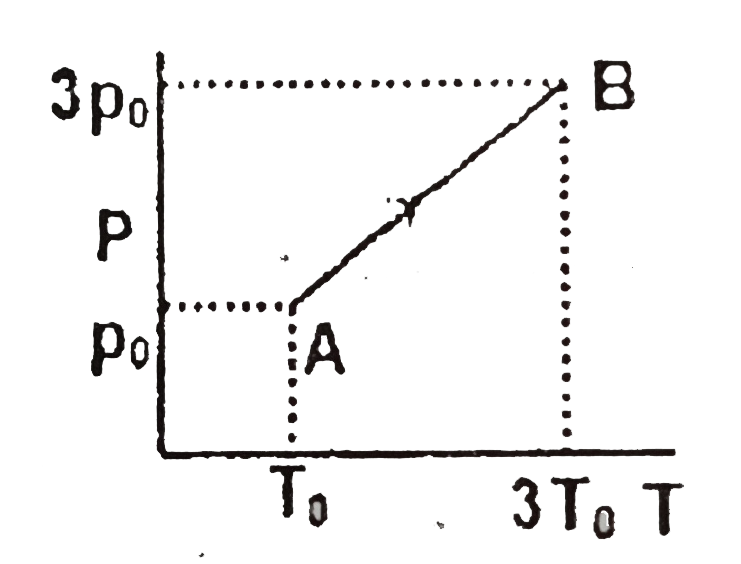
View SolutionTwo moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.
View Solution
