The normal length of a steel spring is 8cm. Keeping one end of the spring fixed at a point, if a weight is attached to the other end, its length becomes 14 cm. The weight is pulled down slightly and then released. Find the time period of oscillation of the spring?
Increase in length of the spring for the mass m is,
l = 14 - 8 = 6 cm.
So, force constant k (force required for a unit increase in length) = mg6dyn⋅cm−1.
Time period, T=2π√mk=2π√mmg6
= 2π√6g=2×3.14×√6980=0.49s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SECTION RELATED QUESTIONS
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
32 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
The end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
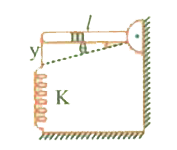
View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View Solution
Knowledge Check
A body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
ATB2TCT2DInfinite as the spring does not oscillateA spring of natural length 80cm with a load has a length of 100cm. If it is slightly pulled down and released its period will be
A3sB0.9sC0.81sD2sCertain weight is attached with a spring. It is pulled down and then released. It oscillates up and down. Its K.E. will be
Amaximum in the middle of the movementBmaximum at the bottomCmaximum just before it is releasedDconstant
The ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
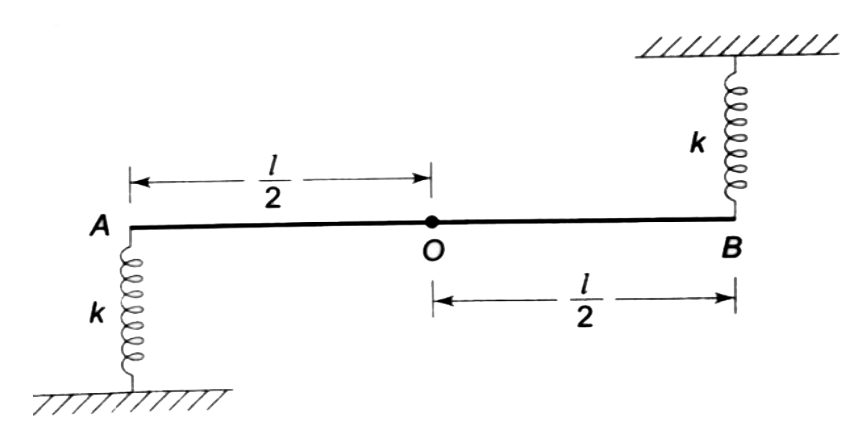
View SolutionOn suspending a heavy block of 2 kg from a massless spring, an extension of 5 cm is produced in the spring. If the block is further pulled down by 10 cm and then released then find the kinetic energy of oscillation of the spring.
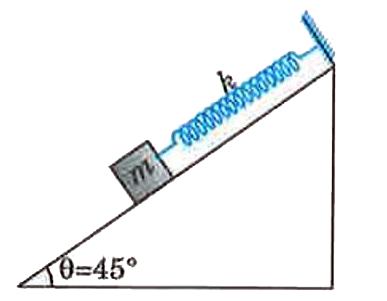
View SolutionA spring of unstretched length 40 cm and spring constant k is attached to a block of mass 1 kg to one of its end. The other end of the spring is fixed on the top of a frictionless inclined plane of inclination θ=45∘ as shown in the figure, so that the spring extends by 3 cm. When the mass is displaced slightly and released the time period of the resulting oscillation is T. Determine the value of 5T close to nearest integer.
View SolutionA light vertical spring is stretched by 0.2cm when a weight of 10g is attached to its free end. The weight is further pulled down by 1cm and released. Compute the frequency and maximum velocity of load.
View SolutionA weightless spring of length 60 cm and force constant 200 N/m is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
View Solution
