Two bodies of mass m1andm2 are suspended from a weightless spring. The force constant of the spring is k. When the bodies are in equilibrium position, the body of mass m1 is taken away from the system such that the equilibrium condition of the system is not disturbed at that very moment. Determine the angular frequency and the amplitude of motion for the body of mass m2.
If increase in length of the spring due to the two masses m1andm2 is l, then
k=(m1+m2)glor,l=(m1+m2)gk
Similarly for the mass m2, increase in length, l2=m2gk. This l2 is the increase in length for the final equilibrium position. So with the mass m1, displacement from the equilibrium position = amplitude of motion
= l−l2=(m1+m2)gk−m2gk=m1gk
Since only the mass m2 vibrates, the angular frequency ω is given by,
ω2=km2or,ω=√km2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SECTION RELATED QUESTIONS
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
32 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
Two mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionTwo masses m1andm2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is
View Solution
Knowledge Check
Two bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
Am2Rm1+m2Bm1Rm1+m2Cm1m2m1+m2RDm1+m2m1RTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
Am2Rm1+m2Bm1Rm1+m2Cm1m2m1+m2RDm1+m2m1RTwo masses m1andm2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is
A√(k/m1)B√(k/m2)C√[k(m1+m2)]D√[k/(m1m2)]
Two masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
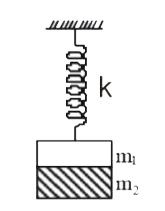
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

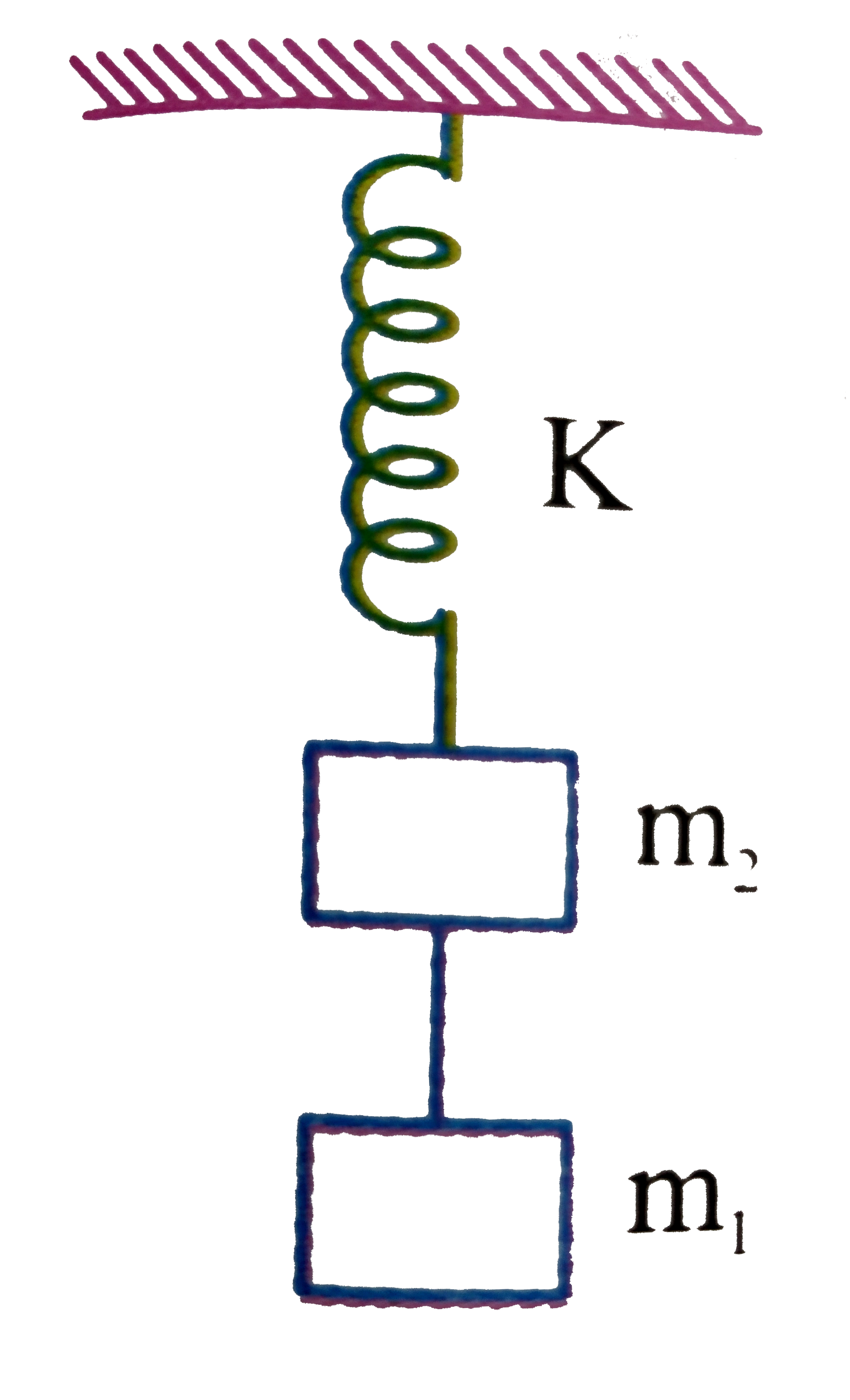
View SolutionTwo masses m1 and m2 are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m1 is removed. Frequency and amplitude of oscillation of m2 are
View SolutionTwo masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
View Solution
