A wooden cylinder floats in water with length h immersed into it. If it is pushed a little inside water and then released, show that it will perform a simple harmonic motion. Calculate the time period of this motion.
Let the cross-sectional area of the cylinder be . According to Archimedes. principle,

weight of the cylinder = weight of the displaced water at equilibrium =
Mass of the cylinder,
If the cylinder is pushed through a distance x inside the water, then an extra buoyant force acts on the cylinder in the upward direction. It tries to bring the cylinder back to its equilibrium position. So the restoring force,
F = extra buoyant force
= weight of the extra water displaced =
Acceleration of the cylinder,
As the motion of the cylinder obeys the equation , it is simple harmonic.
Time period of the motion, .
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
23 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SECTION RELATED QUESTIONS
8 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
Assume that as narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion.
View SolutionA plank rests symmetrically on two cylinders which are separated by a distance of 2l and rotate with uniform speed in opposite direction. If the plank is displaced a little and then released, show that the motion of the plank is simple harmonic. Calculate the period of oscillations of the peak. The co-efficient of friction between the plank and either cylinder is μ.
View Solution
Knowledge Check
The time period of simple harmonic motion depends upon
AamplitudeBenergyCphase constantDmass
The displacement of a particle in simple harmonic motion in one time period is
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
View SolutionConsider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
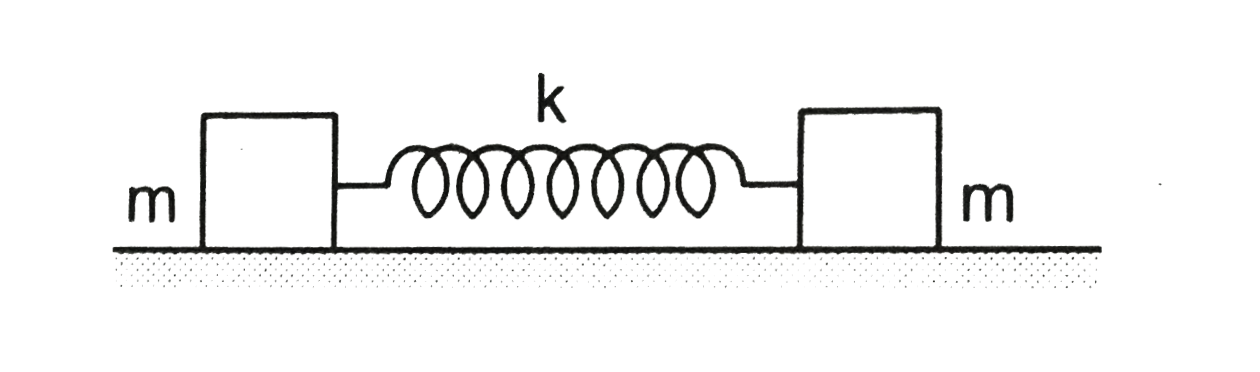
View SolutionConsider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.

View SolutionConsider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.

View SolutionThe average energy in one time period in simple harmonic motion is
View SolutionThe average energy in one time period in simple harmonic motion is
View Solution
