A particle of mass m is attached to one end of a massless spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time t = 0 with an initial velocity u0. When the speed of the particle is 0.5u0, it collides elastically with a rigid wall. After this collision
the speed of the particle when it returns to its equilibrium position is u0
the time at which the particle passes through the equilibrium position for the first time is t=π√mk
the time at which the maximum compression of the spring occurs is t=4π3√mk
the time at which the particle passes through the equilibrium position for the second time is t=5π3√mk
The correct Answer is:A, D
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:COMPREHENSION TYPE
Explore 6 Videos
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:INTEGER ANSWER TYPE
Explore 5 Videos
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:ASSERTION-REASON TYPE
Explore 3 Videos
- ROTATION OF RIGID BODIES Book:CHHAYA PUBLICATIONChapter:ROTATION OF RIGID BODIES Exercise:CBSE SCANNER
Explore 10 Videos
- STATICSBook:CHHAYA PUBLICATIONChapter:STATICSExercise:CBSE SCANNER
Explore 3 Videos
Similar Questions
A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View Solution
Knowledge Check
A small block of mass m is attached to free end of a spring of force cosntant k , whose other end is fixed to a rigid support . The block is lying on a frictionless horizontal plane and it starts movi0ng away from fixed end of the spring a\t t= 0 with intial velocity u When the speed of the block is 0.6μ it collides with a fixed heavy mass elastically. After the collision with a fixed heavy mass elastically . Aftere the collision the time at which the block passes through its equilibrium position for the first time is close to
Aπ√mKB1.86√mKC2√mKD2π√mKA 10 kg mass is connected at one end of a massless spring with force constant k = 1000 N/m, keeping other end fixed in a horizontal plane as shown in the fig. 15.6
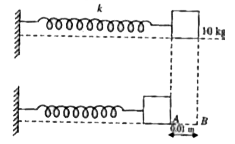 If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
Amω2l0kBmω2l0k−mω2Ckl0k−mω2Dmω2l0k+mω2

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
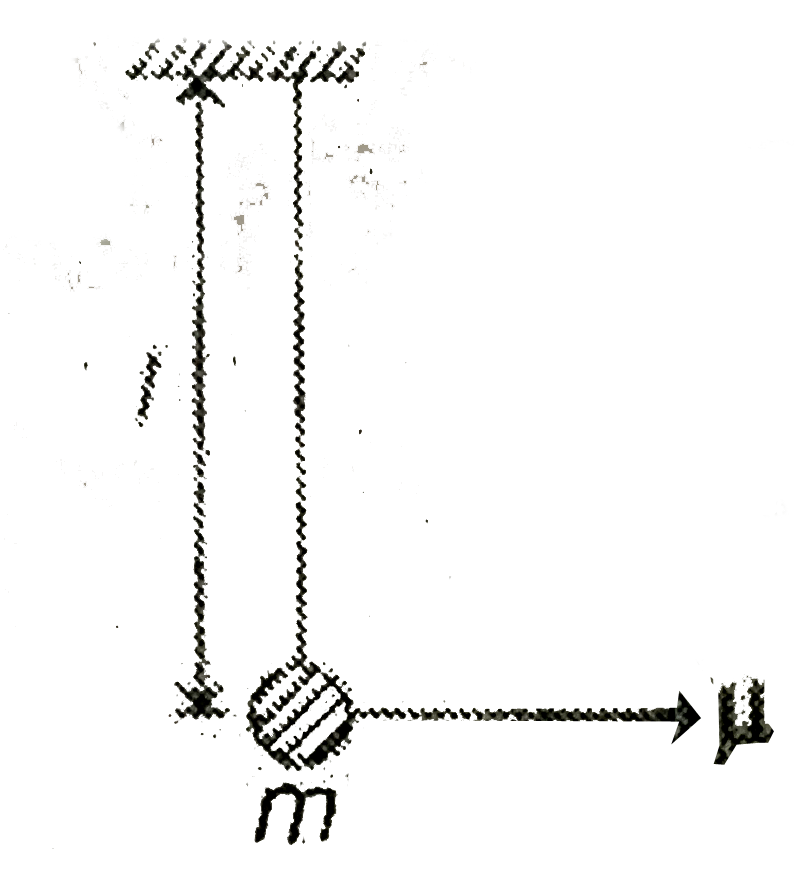
The tension in the string at an instant when acceleration of the particle is horizontal and √3g is
View Solution
