A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
mω2l)k
mω2lk−mω2
mω2lk+mω2
none of these
The correct Answer is:B
To find the final length of the spring when a particle of mass m is attached to one end of a massless spring of spring constant k and natural length l0, and the system is rotated with an angular velocity ω in gravity-free space, we can follow these steps:
1. Identify the Forces Acting on the Mass:
- When the mass is rotated, it experiences a centrifugal force acting outward due to the rotation. This force can be expressed as:
\(
F_{\text{centrifugal}} = m \omega^2 r
\)
- Here, r is the distance from the fixed end of the spring to the mass, which is the final length of the spring (lf).
2. Define the Final Length of the Spring:
- The final length of the spring can be expressed as:
\(
r = l_0 + x
\)
- Where x is the elongation (stretch) of the spring from its natural length l0.
3. Spring Force:
- The spring exerts a restoring force given by Hooke's Law:
\(
F_{\text{spring}} = kx
\)
4. Set Up the Equilibrium Condition:
- In equilibrium, the centrifugal force is balanced by the spring force:
\(
kx = m \omega^2 r
\)
5. Substituting for r:
- Substitute r in the equilibrium equation:
\(
kx = m \omega^2 (l_0 + x)
\)
6. Rearranging the Equation:
- Rearranging gives:
\(
kx - m \omega^2 x = m \omega^2 l_0
\)
- Factor out x:
\(
x(k - m \omega^2) = m \omega^2 l_0
\)
7. Solve for x:
- Solving for x gives:
\(
x = \frac{m \omega^2 l_0}{k - m \omega^2}
\)
8. Calculate the Final Length of the Spring:
- The final length of the spring lf is:
\(
l_f = l_0 + x
\)
- Substitute the expression for x:
\(
l_f = l_0 + \frac{m \omega^2 l_0}{k - m \omega^2}
\)
9. Simplifying the Final Length:
- Factor out l0:
\(
l_f = l_0 \left(1 + \frac{m \omega^2}{k - m \omega^2}\right)
\)
- Combine the terms:
\(
l_f = l_0 \left(\frac{k}{k - m \omega^2}\right)
\)
Final Result:
Thus, the final length of the spring is:
\(
l_f = \frac{k l_0}{k - m \omega^2}
\)
- When the mass is rotated, it experiences a centrifugal force acting outward due to the rotation. This force can be expressed as:
\(
F_{\text{centrifugal}} = m \omega^2 r
\)
- Here, r is the distance from the fixed end of the spring to the mass, which is the final length of the spring (lf).
- The final length of the spring can be expressed as:
\(
r = l_0 + x
\)
- Where x is the elongation (stretch) of the spring from its natural length l0.
- The spring exerts a restoring force given by Hooke's Law:
\(
F_{\text{spring}} = kx
\)
- In equilibrium, the centrifugal force is balanced by the spring force:
\(
kx = m \omega^2 r
\)
- Substitute r in the equilibrium equation:
\(
kx = m \omega^2 (l_0 + x)
\)
- Rearranging gives:
\(
kx - m \omega^2 x = m \omega^2 l_0
\)
- Factor out x:
\(
x(k - m \omega^2) = m \omega^2 l_0
\)
- Solving for x gives:
\(
x = \frac{m \omega^2 l_0}{k - m \omega^2}
\)
- The final length of the spring lf is:
\(
l_f = l_0 + x
\)
- Substitute the expression for x:
\(
l_f = l_0 + \frac{m \omega^2 l_0}{k - m \omega^2}
\)
- Factor out l0:
\(
l_f = l_0 \left(1 + \frac{m \omega^2}{k - m \omega^2}\right)
\)
- Combine the terms:
\(
l_f = l_0 \left(\frac{k}{k - m \omega^2}\right)
\)
Thus, the final length of the spring is:
\(
l_f = \frac{k l_0}{k - m \omega^2}
\)
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4320videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4410videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.419videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
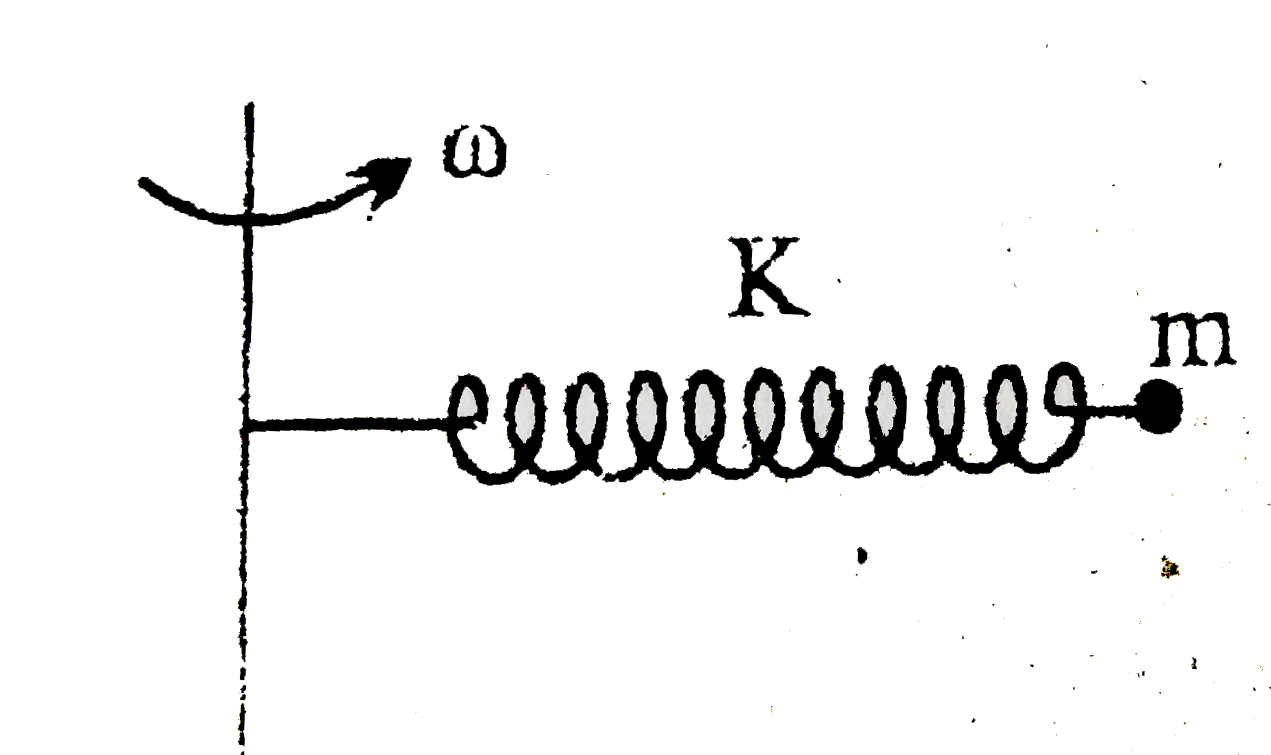 View Solution
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. At the instant the speed of block is maximum the magitude of force exeted by the spring on the block isView Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed isView Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. As the block is coming down, the maximum speed attained by the block isView SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
 View Solution
View SolutionA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
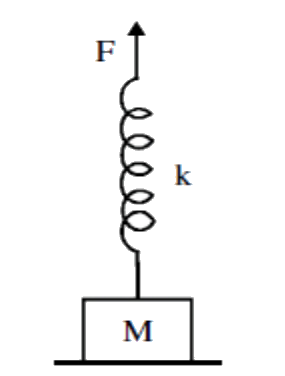 View Solution
View SolutionA horizontal metallic rod of mass 'm' and length 'l' is supported by two vertical identical springs of spring constant 'k' each and natral length l0 A current 'l' is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
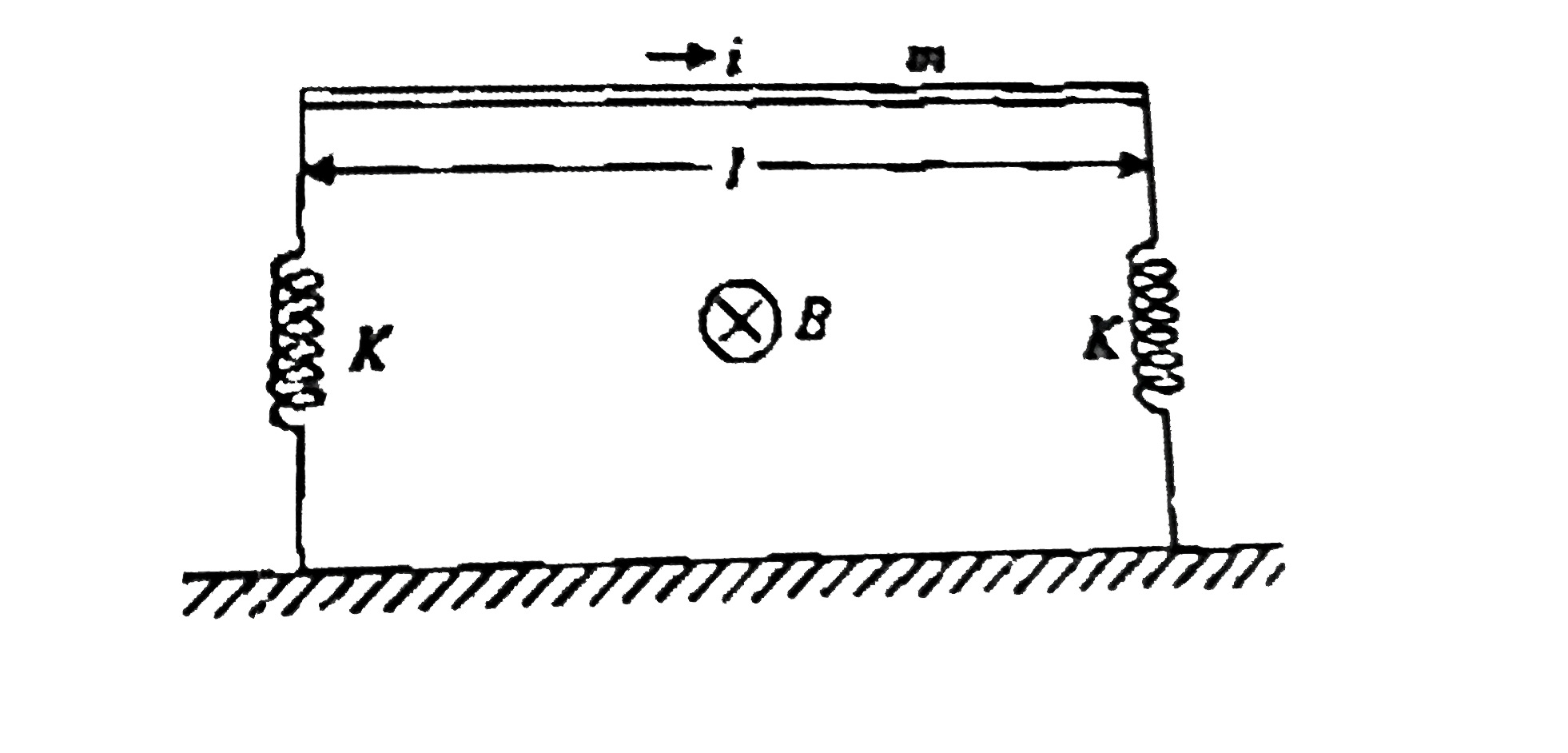 View Solution
View Solution

