A stretched vibrating string is touched at a distance of 13 rd of its length from one end. What would happen to the musical sound emitted ?
The correct Answer is:The point of touch would be a nodal point. So only the 3rd, 6th, 9th, .... Harmonics, which have a node at l3 , would be emitted . No other harmonics have a node at l3 . So , all of them would be suppressed .
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Multiple choice questions (Based on standing wave)
5 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Multiple choice questions (Based on Trabsverse Vibration of string and sonometer)
1 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
- THERMOMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - THERMOMETRYEXERCISE - EXAMINATION ARCHIEVE - WBJEE
1 Videos
Similar Questions
The string in E sonometer is touched lightly at a point one-third of its length from one end. Which harmonics is produced ?
View SolutionA string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibrating ?
View Solution
Knowledge Check
A string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
A400 HzB200 HzC600 HzD300 hzIn the third of vibrations of the string, the distance between extreme end nodes is 2m, then the position of the nodes from the ends will be
A0.667mB0.333mC0.50mD0.25m
A string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibratin ?
View SolutionA string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is 100k then find the value of k.
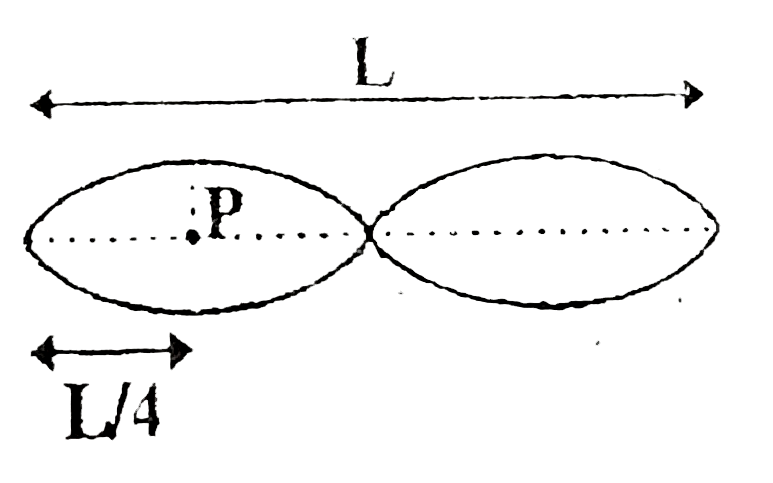
View SolutionA string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is 100k then find the value of k.

View SolutionA string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
View SolutionA string fixed at both ends, is vibrating in a particular mode of vibration. Vibration is such that a point on string is at maximum displacement and it is at a distance of one fourth of length of string from one end. The frequency of vibration in thus mode is 200Hz. What will be the frequency of vibration when it vibrates in next mode such that the same point is at maximum displacement?
View SolutionA string fixed at both ends is vibrating in the lowest mode of vibration for whicha a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. What will be the frequency amitted when it vibrates in the next higher mode such that this point is again a point of maximum displacement.
View Solution
