The area (in sq. units) of the region described by {(x,y):y(2)≤2xandy2≤2xandy≥4x−1}Solution in Telugu
732
564
1564
932
Step by step video & image solution for The area (in sq. units) of the region described by {(x,y):y(2)le2xandy^(2)le2xandyge4x-1} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DEFINITE INTEGRATIONBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DEFINITE INTEGRATIONEXERCISE - EXERCISE 2 (SPECIAL TYPE QUSTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1,2,3 OR 4 GIVEN (SET-1)
6 Videos
- DEFINITE INTEGRATIONBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DEFINITE INTEGRATIONEXERCISE - EXERCISE 2 (SPECIAL TYPE QUSTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1,2,3 OR 4 GIVEN (SET-2)
5 Videos
- DEFINITE INTEGRATIONBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DEFINITE INTEGRATIONEXERCISE - EXERCISE 1D
32 Videos
- DE MOIVRE'S THEOREMBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DE MOIVRE'S THEOREMEXERCISE - EXERCISE 2 SET-4
3 Videos
- DIFFERENTIAL EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 2
15 Videos
Similar Questions
∫√3/3√2/3dx√4−9x2=π36
II ∫1−11(1+x2)2dx=π4+12
View SolutionIf a, b, c are the values of ∫30[x]dx,∫4.50.5[x]dx,∫20[x2]dx then the ascending order of a,b, c is
View SolutionLtn→∞n−1∑r=0nn2+r2=
View SolutionA : (1+i)6+(1−i)6=0
R : If n is a positive integer then (1+i)n+(1−i)n=2(n/2)+1.cosnπ4
View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx
View SolutionThe area (in sq units) of the region {(x,y):y^(2)>=2x and x^(2)+y^(2) =0,y>=0} is
View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View SolutionThe area (in sq units) of the region
A={(x,y):y22≤x≤y+4} is
View SolutionThe area (in sq. units) of the region described by A={(x,y):y≥x2−5x+4,x+y>1,y≤0} is
View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View SolutionThe area (in sq. units) of the region described by {(x,y):y2≤2x and y≥4x−1} is-
View SolutionThe area (in sq units) of the region described by A={(x,y):x2+y2≤1 and y2≤1−x} is :
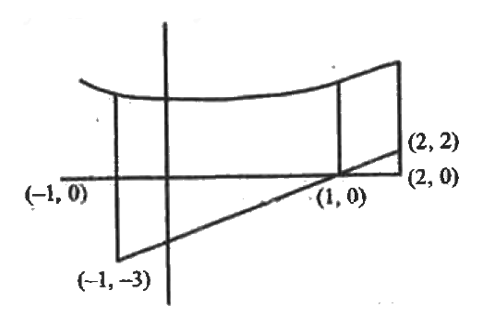
View SolutionThe area (in sq. units) of the region bounded by x=−1,x=2,y=x2+1andy=2x−2 is
View SolutionThe area ( in sq. units ) of the region A={xy|x|+|y∣∣≤1,2y2≥∣∣x∣} is :
View SolutionThe area ( in sq. units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
View Solution
