The area (in sq units) of the region described by ${(x, y) : y^{2} \leq 2 x and y \geq 4 x - 1}$ is

A

$\frac{7}{32}$

B

$\frac{5}{64}$

C

$\frac{15}{64}$

D

$\frac{9}{32}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given region is ${(x, y) : y^{2} \leq 2 x and y \geq 4 x - 1} y^{2} \leq 2 x$ represents a region inside the parabola
$y^{2} = 2 x \dots (i)$
and $y \geq 4 x - 1$ represents a region to the left of the line
$y = 4 x - 1 \dots (ii)$
The point of intersection of the curve (i) and (ii) is
${(4 x - 1)}^{2} = 2 x$
$\Rightarrow 16 x^{2} + 1 - 8 x = 2 x$
$\Rightarrow 16 x^{2} - 10 x + 1 = 0$
$\Rightarrow x = \frac{1}{2}, \frac{1}{8}$
At $x = \frac{1}{2}, y = 1$
At $x = \frac{1}{8}, y = \frac{- 1}{2}$
$∴$ The points where these curves intersect, are $(\frac{1}{2}, 1)$ and $(\frac{1}{8}, - \frac{1}{2})$

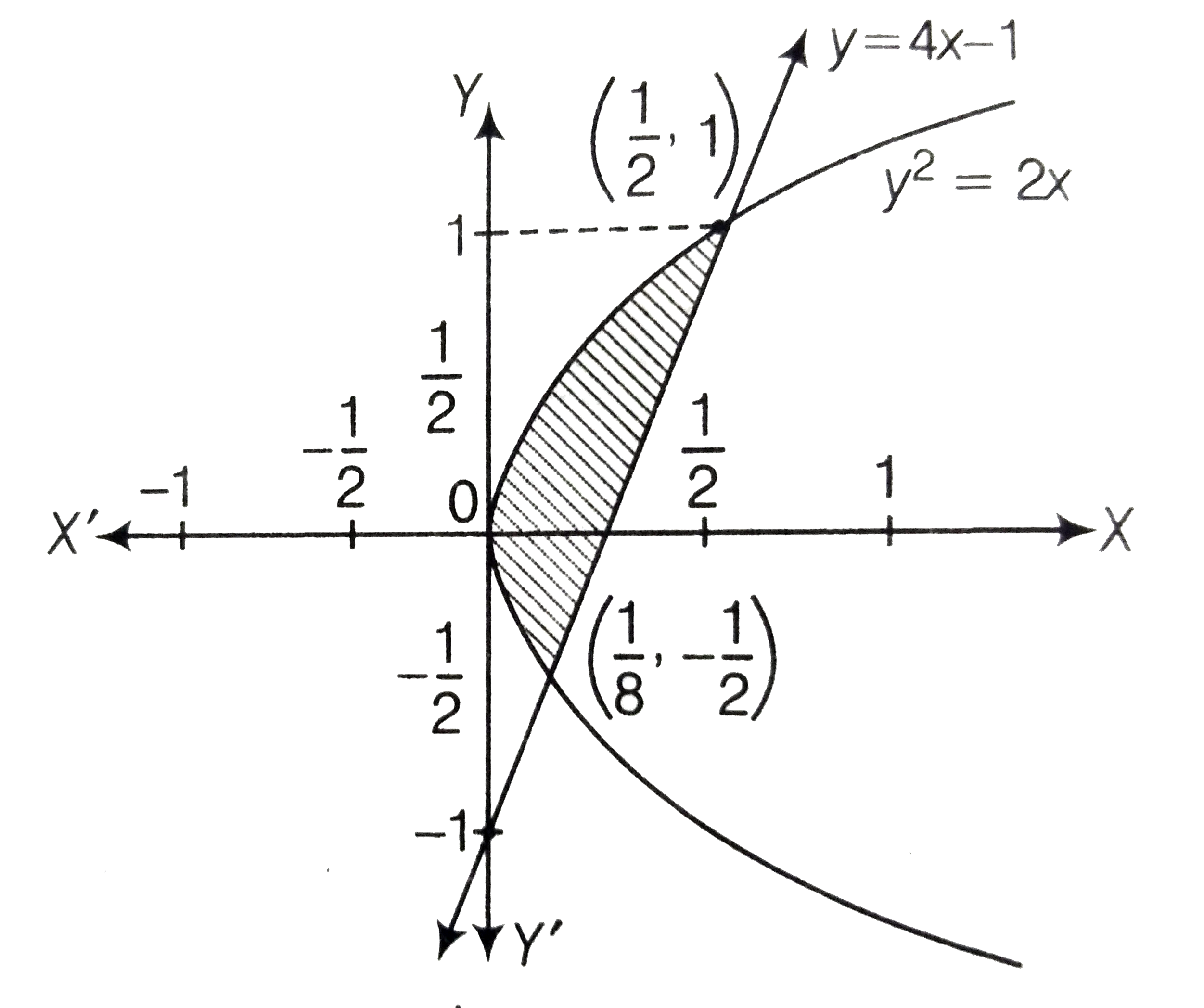
Hence, required area $= \int_{- 1 / 2}^{1} (\frac{y + 1}{4} - \frac{y^{2}}{2}) d y$
$= \frac{1}{4} {(\frac{y^{2}}{2} + y)}_{- 1 / 2}^{1} - \frac{1}{6} {(y^{3})}_{- 1 / 2}^{3}$
$= \frac{1}{4} {(\frac{1}{2} + 1) - (\frac{1}{8} - \frac{1}{2})} - \frac{1}{6} {1 + \frac{1}{8}}$
$= \frac{1}{4} {\frac{3}{2} + \frac{3}{8}} - \frac{1}{6} {\frac{9}{8}} = \frac{1}{4} \times \frac{15}{8} - \frac{3}{16} = \frac{9}{32}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area (in square units) of the region described by ${(x, y) : y^{2} \leq 2 x and y \leq 4 - x}$ is
A $\frac{7}{32}$
B $\frac{5}{64}$
C $\frac{15}{64}$
D $18$
The area (in sq units) of the region described by ${(x, y) : y^{2} \leq 2 x and y \geq 4 x - 1}$ is
A $\frac{7}{32}$
B $\frac{5}{64}$
C $\frac{15}{64}$
D $\frac{9}{32}$
The area (in sq units) of the region described by $A = {(x, y) : x^{2} + y^{2} \leq 1$ and $y^{2} \leq 1 - x}$ is :
A $\frac{π}{2} + \frac{4}{3}$
B $\frac{π}{2} - \frac{4}{3}$
C $\frac{π}{2} - \frac{2}{3}$
D $\frac{π}{2} + \frac{2}{3}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -Exercise 2

Home
Ask Doubt
Profile