In ΔOAB, E is the mid point of AB and F is a point on OA such that OF=2FA. If C is the point of intersection of OE and BF, then find the ratios OC : CE and BC : CF are Solution in Telugu
The correct Answer is:OC:CE=4:1
BC:CF=3:2
Step by step video, text & image solution for In DeltaOAB, E is the mid point of AB and F is a point on OA such that OF=2FA. If C is the point of intersection of OE and BF, then find the ratios OC : CE and BC : CF are by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SRISIRI PUBLICATIONCHAPTER - ADDITION OF VECTORSEXERCISE - SPQ7videos
ADDITION OF VECTORS
- BOOK - SRISIRI PUBLICATIONCHAPTER - ADDITION OF VECTORSEXERCISE - 2 D (SAQ)13videos
ADDITION OF VECTORS
- BOOK - SRISIRI PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - 10.5 MAXIMA AND MINIMA - VSAQ . SAQ (SPQ)1videos
APPLICATIONS OF DERIVATIVES
Similar Questions
Let ¯a=¯i+2¯j+3¯kand¯b=3¯i+¯j. . Find a unit vector in the direction of ¯a+¯b
02:51View SolutionIf ¯i,¯j,¯k are unit vectors along the positive directions of the coordinate axes, then shown that the four points 4¯i+5¯j+¯k,−¯j−¯k,3¯i+9¯j+4¯kand−4¯i+4¯j+4¯k are coplanar
05:14View SolutionFind a point on the curve y=x3, when the tangent is parallel to the chord joining (1,1), (3,27).
02:30View SolutionIf D E and F be the mid ponts of the sides BC, CA and AB respectively of the △ABC and O be any point, then prove that −−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF
05:24View SolutionE और F क्रमश: त्रिभुज ABC की बराबर भुजाओ AB और AC के मध्यें-बिंदु है दर्शाइए की BF=CE है
05:45View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
04:28View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA04:26View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the mid-points of opposite sides. If O be any point in the plane, then show that −−→OA+−−→OB+−−→OC+−−→OD=4−−→OE.
05:52View SolutionIn a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?
 02:15View Solution
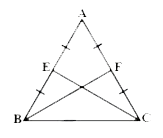
02:15View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
 01:59View Solution
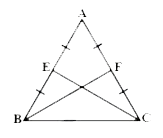
01:59View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
 05:57View Solution
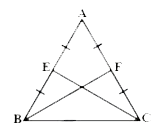
05:57View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
 08:57View Solution
08:57View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC (see figure)
Show that BF = CE.
 04:23View Solution
04:23View SolutionIn ΔOAB, E is the mid point of AB and F is a point on OA such that OF=2FA. If C is the point of intersection of OE and BF, then find the ratios OC : CE and BC : CF are
03:07View SolutionIn ΔOAB, E is the midpoint of AB and F is a point on OA such that OF = 2FA. If C is the point of intersection of ¯¯¯¯¯¯OEand¯¯¯¯¯¯BF, then find the ratios OC : CE and BC : CF.
08:57View Solution

