In a quadrilateral ABCD , if the midpoints of one pair of opposite sides and the point of intersection of the diagonals are collinear , using vector methods , prove that the quadrilateral ABCD is a trapezium .
The correct Answer is:¯¯¯¯¯¯AB is parallel to ¯¯¯¯¯¯CD
Topper's Solved these Questions
- ADDITION OF VECTORSBOOK - SRISIRI PUBLICATIONCHAPTER - ADDITION OF VECTORSEXERCISE - SPQ
7 Videos
- ADDITION OF VECTORSBOOK - SRISIRI PUBLICATIONCHAPTER - ADDITION OF VECTORSEXERCISE - 2 D (SAQ)
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - SRISIRI PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - 10.5 MAXIMA AND MINIMA - VSAQ . SAQ (SPQ)
1 Videos
Similar Questions
The midpoint of two opposite sides of a quadrilateral and the midpoint of the diagonals are the vertices of a parallelogram. Prove that using vectors.
View SolutionThe midpoint of two opposite sides of a quadrilateral and the midpoint of the diagonals are the vertices of a parallelogram. Prove that using vectors.
View Solution
Knowledge Check
In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
Complete each of the following, so as to make a true statement:
(i) A quadrilateral has ______sides.:
(ii) A quadrilateral has ______angles.:
(iii) A quadrilateral has ______vertices, no three of which are ______:
(iv) A quadrilateral has ______diagonals.:
(v) The number of pairs of adjacent angles of a quadrilateral is ______:
(vi) The number of pairs of opposite angles of a quadrilateral is ______:
(vii) The sum of the angles of a quadilateral is ______:
(viii) A diagonal of a quadrilateral is a line segment that joins two ______vertices of the quadrilateral.:
(ix) The sum of the angles of a quadrilateral is ______ right angles. :
(x) The measure of each angle of a convex quadrilateral is ______ 180 ∘ .:
(xi) In a quadrilateral the point of intersection of the diagonals lies in ______ of the quadrilateral.:
(xii) A point is in the interior of a convex quadrilateral, if it is in the ______ of its two opposite angles.:
(xiii) A quadrilateral is convex if for each side, the remaining ______ lie on the same side of the line containing the side.
View SolutionComplete each of the following, so as to make a true statement: A quadrilateral has ............ sides A quadrilateral has ............ angles. A quadrilateral has ............ vertices, no three of which are.... A quadrilateral has ............ diagonals. The number of pairs of adjacent angles of a quadrilateral is ...... The number of pairs of opposite angles of a quadrilateral is ...... The sum of the angles of quadrilateral is..... A diagonals of quadrilateral is a line segment that joins two ..... vertices of the quadrilateral. The sum of the angles of a quadrilateral is ......... right angles. The measure of each angle of a convex quadrilateral is ...... 1800. In a quadrilateral the point of intersection of the diagonals lie lies in .... of the quadrilateral. A point is in the interior of a convex quadrilateral, if it is in the ....... of its two opposite angles. A quadrilateral is convex if for each side, the remaining.... lie on the same side of the line containing the side.
View SolutionIn parallelogram ABCD, diagonals AC and BD are equal. Find the measure of ∠ ABC and prove that the quadrilateral ABCD is a rectangle.
View SolutionABCD is a quadrilateral and BD is one of its diagonals, as shown in the figure. Prove that quadrilateral ABCD is a parallelogram, also find its area.
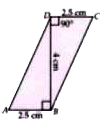
View SolutionIf the quadrilateral formed by joining the mid points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.
View SolutionABCD is a quadrilateral and O is point in its plabe such that →OA+→OB+→OC+→OD=0 Show that O is the point of intersection of the lines joining the mid points of the opposite sides of quadrilateral ABCD.
View Solution
