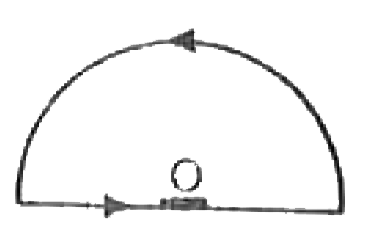
A wheel of radius 8 units rolls along the diameter of a semicircle of radius 25 units; it bumps into this semicircle. What is the length of the portion of the diameter that cannot be touched by the wheel? 12 (b) 15 (c) 17 (d) 20
Step by step video & image solution for A wheel of radius 8 units rolls along the diameter of a semicircle of radius 25 units; it bumps into this semicircle. What is the length of the portion of the diameter that cannot be touched by the wheel? 12 (b) 15 (c) 17 (d) 20 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
In a quadrant of a circle of diameter 4 units semicircles are drawn as shown. The radius of the smaller circle (B) is
View SolutionA thin wire of length l=1m is shipped into a semicircle with diameter. Calculate the force per unit length at the mid-point of the diameter when it carries a current I = 8A.
View Solution
Knowledge Check
A rectangle is inscribed in a semicircle of radius 1 unit. If its two vertices lie on the diameter, for largest size, then its dimensions are
ALength =√2, breadth =1√2BLength =√3, breadth =12CLength =2√3√2, breadth =13DLength =1√2, breadth =√2Two circles with centers A and B and radius 2 units touch each other externally at 'C' and radius 2 units meets other two at D and E. Then the area of the quadrilateral ABDE is :
A2√2 sq. unitB3√3 sq. unitC3√2 sq. unitD2√3 sq. unitIf the lengths of the sides of a triangle are 8, 15 and 17 units, the R the circum-radius is :
A9.0B8.5C8.0D7.5
The radius of a car wheels is 15 units
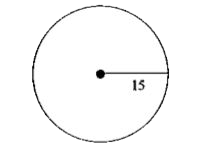
What is the area of the wheel?
View SolutionGiven: AC has length 5, semicircle AB has radius 1, semicircle BC has diameter 3. What percent of the the big circle is shaded ?
View SolutionIn a circle of radius 3 units, a diameter AB intersects a chord of length 2 units perpendicularly at P. If AP>BP, then what is the ratio of AP to BP?
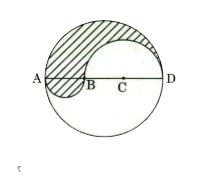
View SolutionIn the figure given below, ABCD is the diameter of a circle of radius 9 cm. The lengths AB, BC and CD are equal. Semicircles are drawn on AB and BD as diameters as shown in the figure. What is the area of the shaded region ?
View SolutionA semicircle is inscribed inside a rectangle in such a way, so that the diameter semicides with the length of the rectangle. If the area of the semicircle is 50π, then what is area of the rectangle?
(a)200
(b)175
(c)150
(d)125
View Solution
