In a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
To find the radius of the semicircle inscribed in triangle ABC, where the diameter lies on side c, we can follow these steps:
Step 1: Understand the Geometry
In triangle ABC, let:
- Side BC = a
- Side AC = b
- Side AB = c
- The area of triangle ABC = Δ
Step 2: Divide the Triangle
The semicircle is inscribed such that its diameter lies along side c (AB). We can divide triangle ABC into two smaller triangles by drawing a line from point C to the midpoint of side AB.
Step 3: Calculate Areas of Smaller Triangles
Let O be the midpoint of side c (AB). The area of triangle AOB can be calculated as:
Area of △AOB=12×AB×hA=12×c×hA
where hA is the height from point C to line AB.
Similarly, the area of triangle BOC can be calculated as:
Area of △BOC=12×BC×hB=12×a×hB
Step 4: Relate Areas to the Semicircle
The area of triangle ABC can be expressed as the sum of the areas of triangles AOB and BOC:
Δ=Area of △AOB+Area of △BOC
Δ=12×c×hA+12×a×hB
Step 5: Express Heights in Terms of Radius
The height from point C to line AB can be expressed in terms of the radius r of the semicircle. Since the semicircle is inscribed, we can relate the heights to the radius:
hA=randhB=r
Step 6: Substitute Heights into Area Equation
Substituting the heights into the area equation gives:
Δ=12×c×r+12×a×r
Δ=r2(c+a)
Step 7: Solve for Radius r
Rearranging the equation to solve for r:
r=2Δa+c
Final Result
Thus, the radius of the semicircle inscribed in triangle ABC is:
r=2Δa+c
In triangle ABC, let:
- Side BC = a
- Side AC = b
- Side AB = c
- The area of triangle ABC = Δ
The semicircle is inscribed such that its diameter lies along side c (AB). We can divide triangle ABC into two smaller triangles by drawing a line from point C to the midpoint of side AB.
Let O be the midpoint of side c (AB). The area of triangle AOB can be calculated as:
Area of △AOB=12×AB×hA=12×c×hA
where hA is the height from point C to line AB.
Area of △BOC=12×BC×hB=12×a×hB
The area of triangle ABC can be expressed as the sum of the areas of triangles AOB and BOC:
Δ=Area of △AOB+Area of △BOC
Δ=12×c×hA+12×a×hB
The height from point C to line AB can be expressed in terms of the radius r of the semicircle. Since the semicircle is inscribed, we can relate the heights to the radius:
hA=randhB=r
Substituting the heights into the area equation gives:
Δ=12×c×r+12×a×r
Δ=r2(c+a)
Rearranging the equation to solve for r:
r=2Δa+c
Thus, the radius of the semicircle inscribed in triangle ABC is:
r=2Δa+c
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type24videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
In Figure, C is the center of the semicircle, and the area of the semicircle is 8π. What is the area of triangle ABC in terms of θ ?
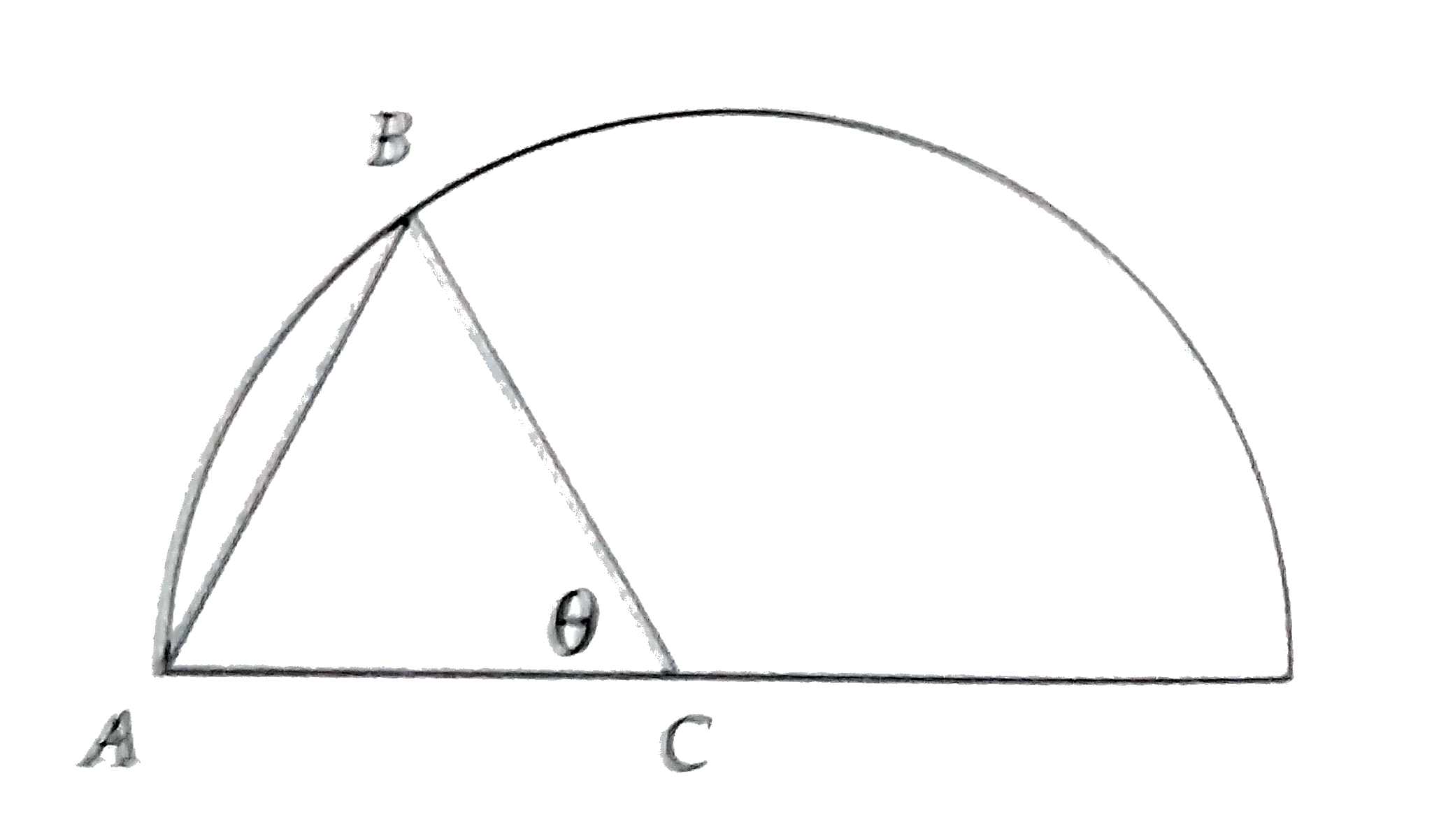 View Solution
View SolutionIn ABC, as semicircle is inscribed, which lies on the side ⋅ If x is the lengthof the angle bisector through angle C, then prove that the radius of the semicircle is xsin(C2).
View SolutionA small card is in the shape of an isosceles triangle with a semicircle on its base. If the diameter of the semicircle is 6 cm, and the hright of the triangle is 3 cm, find the area of the card.
View SolutionA circle is inscribed in an equilateral triangle of side a. Find the area of any square inscribed in this circle.
View SolutionIf a,b and c are sides of a ritht triangle where c is the hypotenuse, prove that the radius of the circle which touches the sides of the triangle is r=a+b−c2.
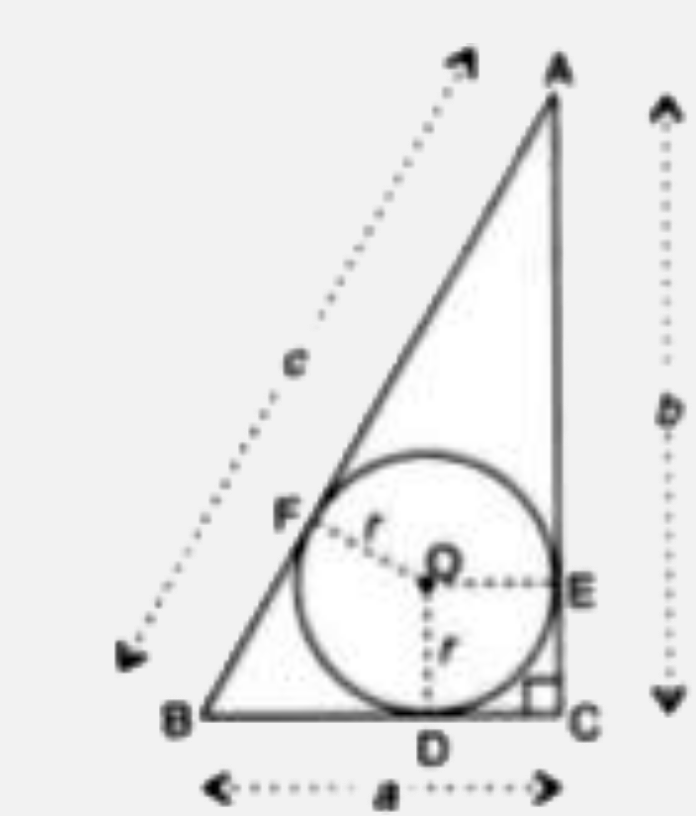 View Solution
View SolutionAB is the diameter of a semicircle k,C is an arbitrary point on the semicircle (other than A or B) and S is the centre of the circle inscribed into triangle ABC, then measure of-
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View SolutionThe in-radius of the triangle whose sides are 3,5,6,is
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionA circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is ______.
View Solution

