Two parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB depends on the radius of the circle. depends on the center of the circle. depends on the slopes of three tangents. is always constant
Step by step video & image solution for Two parallel tangents to a given circle are cut by a third tangent at the points Aa n dBdot If C is the center of the given circle, then /_A C B depends on the radius of the circle. depends on the center of the circle. depends on the slopes of three tangents. is always constant by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Two parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB depends on the radius of the circle. depends on the center of the circle. depends on the slopes of three tangents. is always constant
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.
View Solution
Knowledge Check
In the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
 AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+ACIn the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
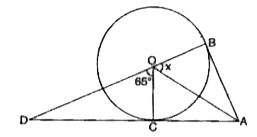 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
The line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4 . Then find the radius of the circle.
View SolutionThe line y=x is a tangent at (0,0) to a circle of radius unity. The center of the circle is
View SolutionIf we draw a tangents to a circle at a given point on it, when the centre of the circle is known, then the angle between the tangent and radius of the circle is
View Solution(iii)If two circles cut a third circle orthogonally; then the radical axis of two circle will pass through the center of the third circle .
View SolutionThe radical center of three given circles will be the center of a fourth circle which cuts all the three circles orthogonally.
View Solution
