If we draw a tangents to a circle at a given point on it, when the centre of the circle is known, then the angle between the tangent and radius of the circle is
60∘
180∘
90∘
120∘
To solve the problem regarding the angle between the tangent to a circle at a given point and the radius of the circle, we can follow these steps:
1. Identify the Circle and Key Points:
- Let the center of the circle be denoted as O.
- Let the point where the tangent touches the circle be denoted as P.
- The tangent line at point P will be denoted as line AB.
2. Understand the Relationship:
- By the properties of a circle, the radius drawn to the point of tangency (in this case, OP) is always perpendicular to the tangent line at that point.
3. Apply the Perpendicularity Property:
- Since OP is the radius and it meets the tangent line AB at point P, we can conclude that the angle ∠OPA (the angle between the radius and the tangent) is 90∘.
4. Conclusion:
- Therefore, the angle between the tangent AB and the radius OP is 90∘.
Final Answer:
The angle between the tangent and the radius of the circle is 90∘.
---
- Let the center of the circle be denoted as O.
- Let the point where the tangent touches the circle be denoted as P.
- The tangent line at point P will be denoted as line AB.
- By the properties of a circle, the radius drawn to the point of tangency (in this case, OP) is always perpendicular to the tangent line at that point.
- Since OP is the radius and it meets the tangent line AB at point P, we can conclude that the angle ∠OPA (the angle between the radius and the tangent) is 90∘.
- Therefore, the angle between the tangent AB and the radius OP is 90∘.
The angle between the tangent and the radius of the circle is 90∘.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - self assesment -2 (Fill in the blanks)
3 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - self assesment -2 (Very Short Answer Type Questions)
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - self assesment -1 (IV. Long Answer Type Questions)
2 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT
5 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
Similar Questions
Knowledge Check
The distance of point A from the centre of the circle is 5 cm. The length of the tangent is 4 cm. The radius of the circle is :
A3 cmB4 cmC5 cmD8 cmIf a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
A30∘B60∘C90∘D120∘
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.

View SolutionDraw a circle of radius 3 cm. Mark a point P on the circle. Draw tangent to the circle through point P using the centre of the circle Analysis
A circle of radius 3 cm can be drawn. Let the cemntre of the given circle be O and line l be the required tangent
We know, converse of tangent theorem states that , 'A line perpendicular to radius at its outer end is tangent .
∴ We construct perpendicular to radius OP at point, then line l is the required tangent .

View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View SolutionConsider two circle of radius 3 and 1 and distance between the centre of these two circle is 5, then length of external common tangent is
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
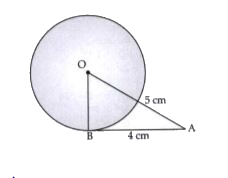
View SolutionThe length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle ?
View Solution

