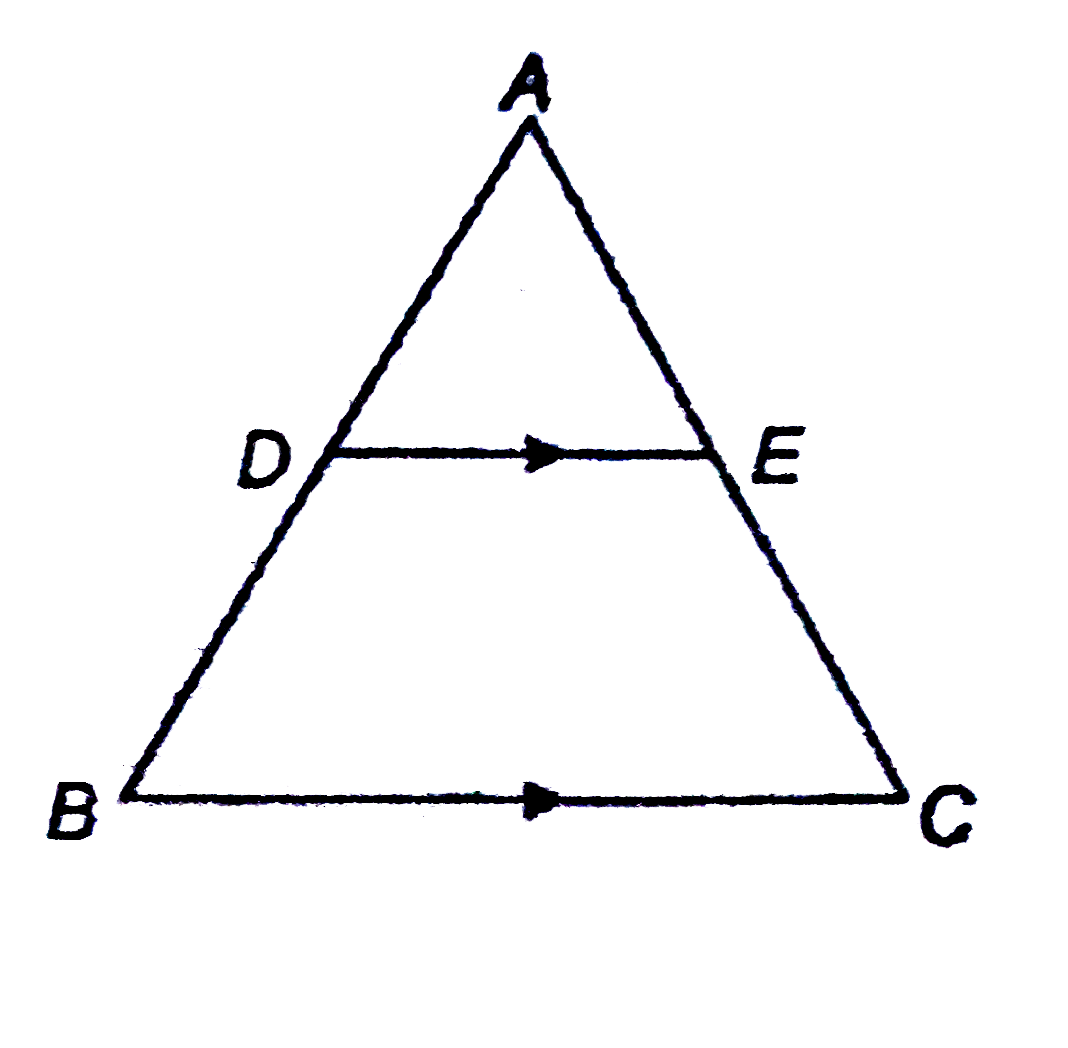
In the adjoining figure DE||BE and D divides AB in the ratio 2:3 find.
(i) AEEC (ii) AEAC
Video Solution
Text Solution
Since DE||BC, hence by Thale's theorem.
ADDB=AEEC
Also. ADDB=23
Therefore, from (1) and (2) , ADDB=AEEC=23
(ii) AEAC=AEAE+EC=AE/ECAE/EC+EC/EC=2323+1=⎛⎝2353⎞⎠=25
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a23videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining figure ABBC=ADDF, where EBCF is a square . Find the ratio of AEEF :
 A(1±√7)3B(1−√7)2C(1+√5)2D(1±√5)2
A(1±√7)3B(1−√7)2C(1+√5)2D(1±√5)2
In the figure, DE∣∣BCandAE:EC=3:7. Find
View SolutionIn the adjoining figure, if AB||CD||FE, then find x and AE.
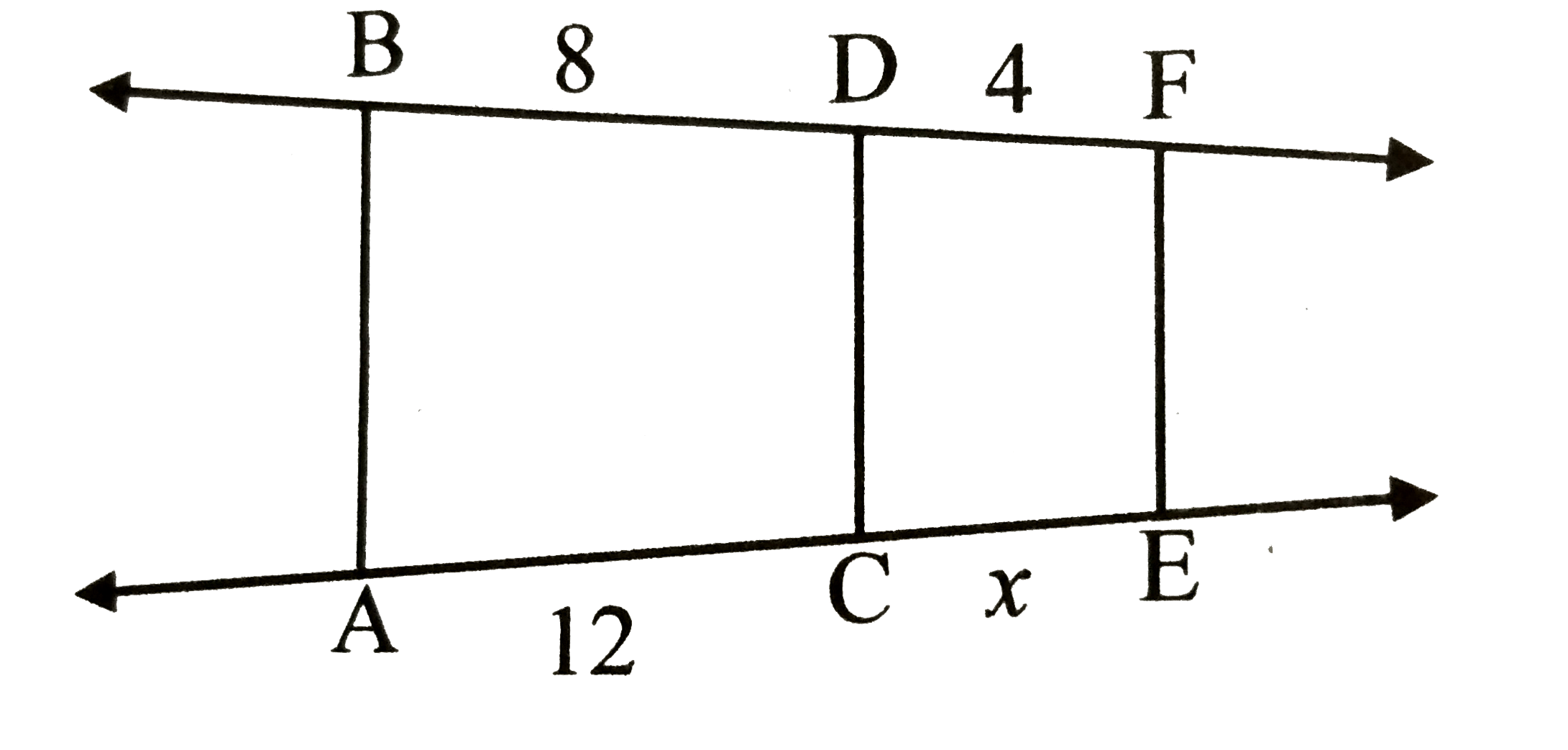 View Solution
View SolutionIn the adjoining figure, if AB || CD || FE, then find x and AE.
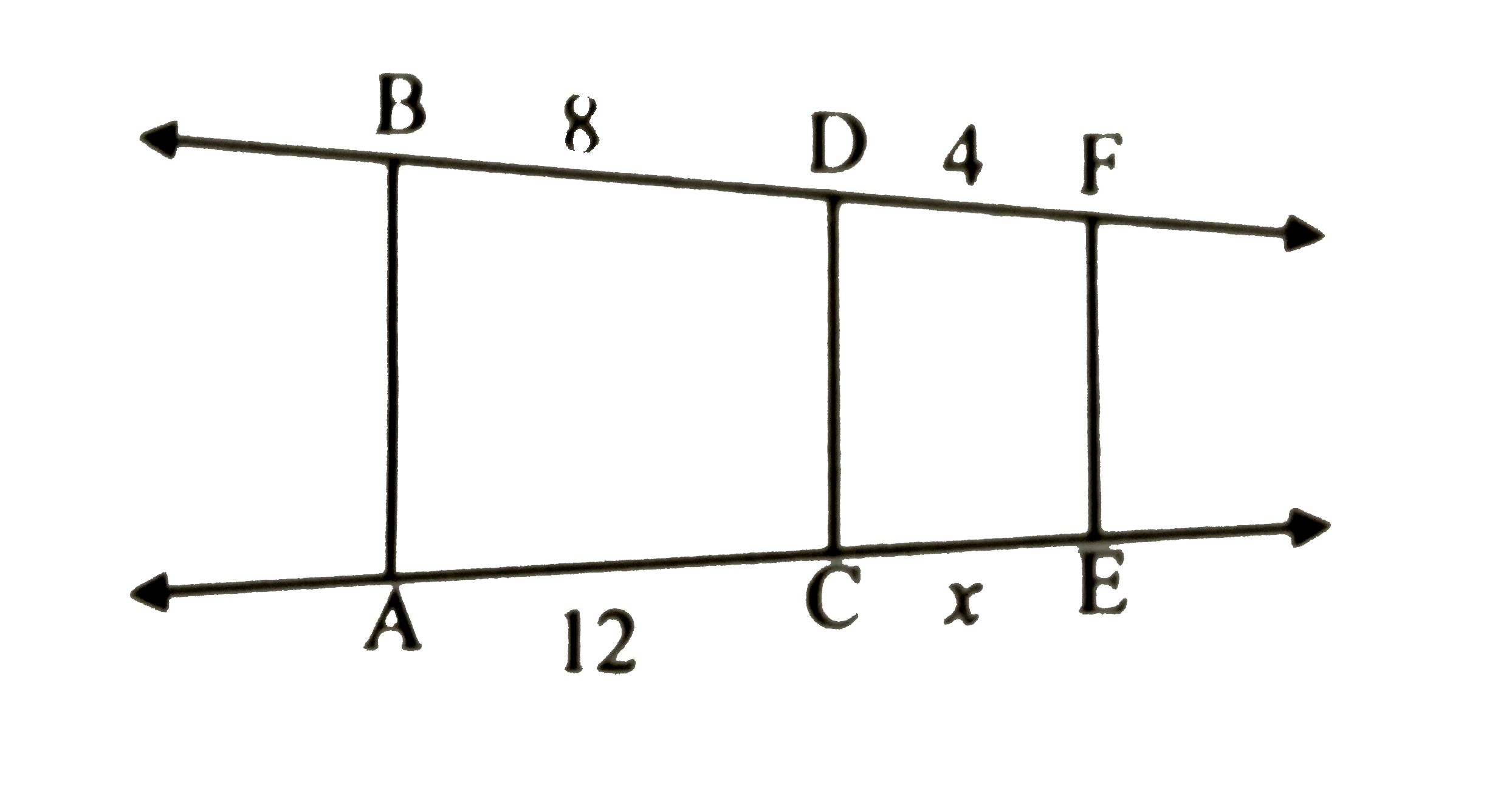 View Solution
View SolutionIn the adjoining figure,seg DE||side AC and seg DC ||side AP.
Prove that BEEC=BCCP.
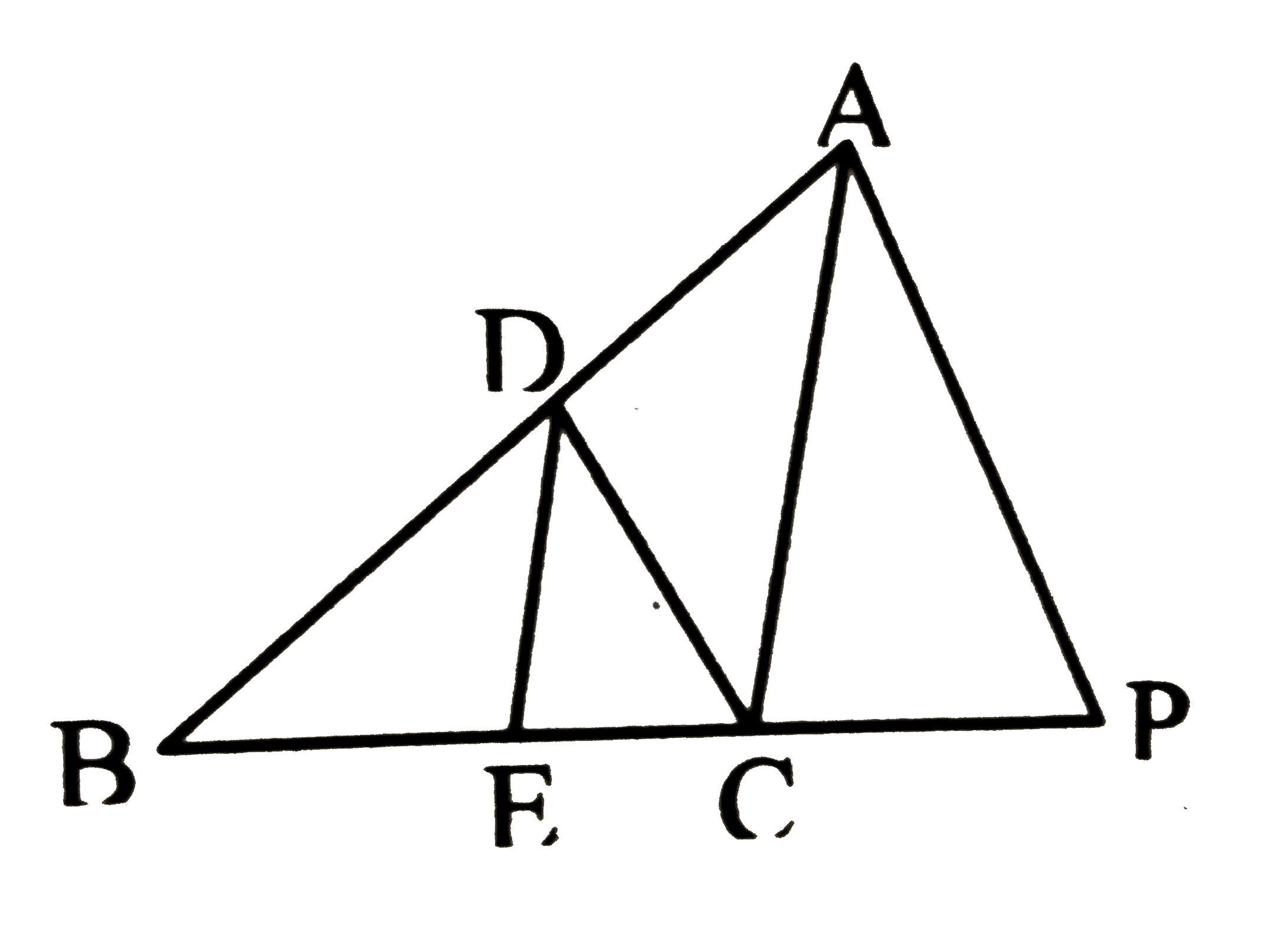 View Solution
View SolutionIn the following figure, FD||BC||AE and AC||ED. Find the value of x.
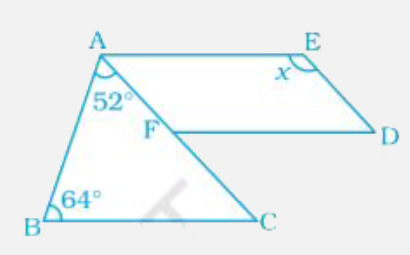 View Solution
View SolutionIn the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.
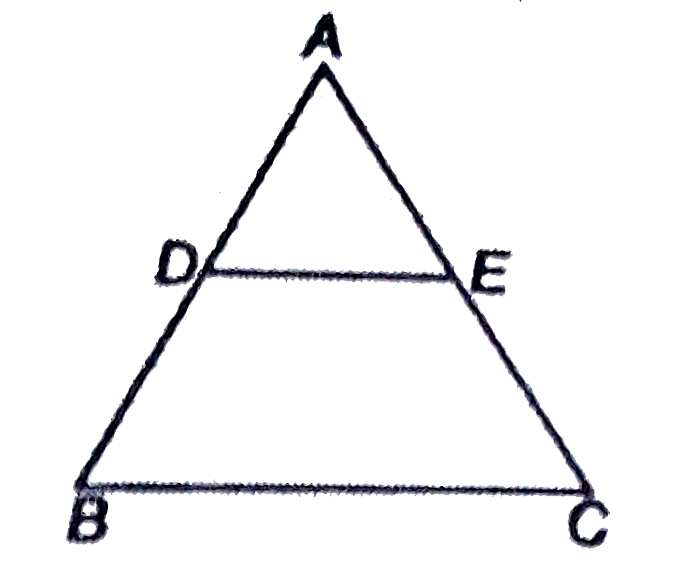 View Solution
View SolutionIn the given figure, AB∣∣EC,AB=AC and AE bisects ∠DAC. Prove that:
View Solution