In the given figure △ACB~△APQ. If BC= 8cm , PQ = 4cm BA= 6.5 cm, AP = 2.8 cm, find CA and AQ.
To solve the problem, we will use the property of similar triangles. Since triangle ACB is similar to triangle APQ, we can set up a proportion based on their corresponding sides.
1. Write down the similarity ratio:
Since triangle ACB ~ triangle APQ, we can write the ratios of the corresponding sides:
ACAP=BCPQ=ABAQ
2. Substitute known values:
We know:
- BC=8cm
- PQ=4cm
- BA=6.5cm
- AP=2.8cm
Therefore, we can set up the first ratio:
AC2.8=84
3. Simplify the ratio:
The ratio 84 simplifies to 2:
AC2.8=2
4. Cross-multiply to find AC:
Cross-multiplying gives:
AC=2×2.8=5.6cm
5. Now, find AQ using the second ratio:
We can use the second ratio:
ABAQ=84
Substituting the known values:
6.5AQ=2
6. Cross-multiply to find AQ:
Cross-multiplying gives:
6.5=2×AQ⟹AQ=6.52=3.25cm
Final Results:
- CA=5.6cm
- AQ=3.25cm
Since triangle ACB ~ triangle APQ, we can write the ratios of the corresponding sides:
ACAP=BCPQ=ABAQ
We know:
- BC=8cm
- PQ=4cm
- BA=6.5cm
- AP=2.8cm
AC2.8=84
The ratio 84 simplifies to 2:
AC2.8=2
Cross-multiplying gives:
AC=2×2.8=5.6cm
We can use the second ratio:
ABAQ=84
Substituting the known values:
6.5AQ=2
Cross-multiplying gives:
6.5=2×AQ⟹AQ=6.52=3.25cm
- CA=5.6cm
- AQ=3.25cm
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In the figure ΔABC~ΔPQ. If BC=8cm,PQ=4cm,AP=2.8cm, find CA :
 A8 cmB6.5cmC5.6 cmDnone of these
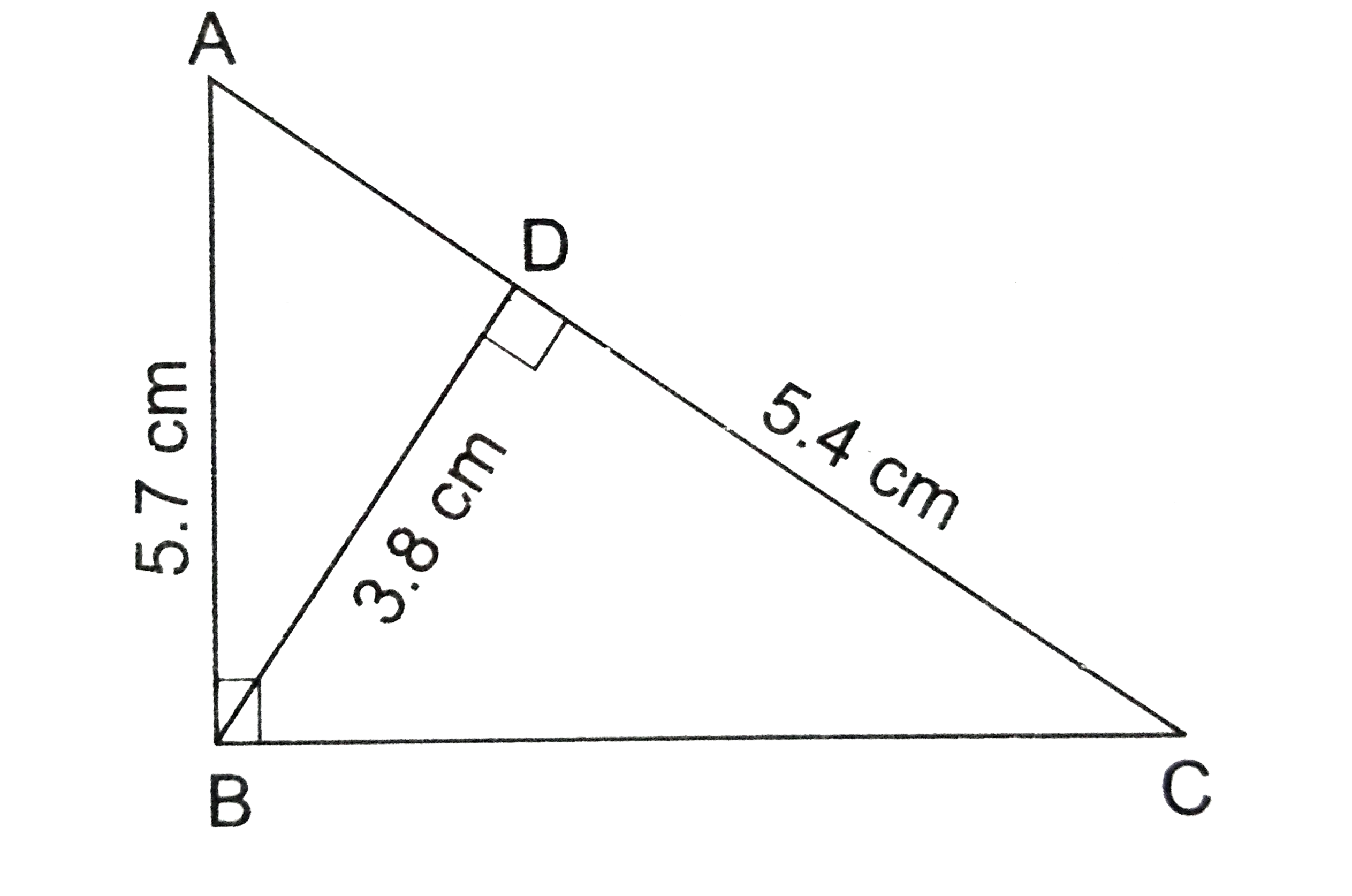
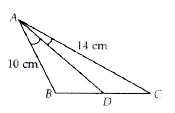
A8 cmB6.5cmC5.6 cmDnone of theseIn the given figure , Ad is the bisector of ∠BAC. If AB = 10 cm , AC = 14 cm and BC = 8 cm , find BD and DC respectively .
 A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm
A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cmIn figure ,DE||BC in triangle ABC such that BC = 8 cm , AB = 6 cm and DA = 1.5 cm .find DE.
 A2 cmB3 cmC4 cmD5 cm
A2 cmB3 cmC4 cmD5 cm
In the given figure O is the centre of the circle. If AB = 16 cm, CP = 6 cm, PD = 8 cm and AP > PB then what will be the value of AP.

View SolutionIn given figure, if ∠A=∠C, AB= 6 cm, BP = 15 cm, AP = 12 cm and CP= 4 cm, then find the lengths of PD and CD.

View SolutionIn the given figure, ΔOAB~ΔOCD. If AB=8cm,BO=6.4cm,OC=3.5cmandCD=5cm find (i) OA (ii) DO.
View SolutionIn the given figure find PQ ? If AB = 8 cm, CD = 6 cm, if Radius of circle = 5 cm
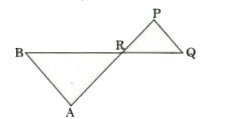
View SolutionIn the figure given below, ΔABR~ΔPQR. If PQ = 3 cm, AB = 6 cm, BR = 8.2 cm and PR = 5.2 cm, then QR and AR are respectively
View Solution