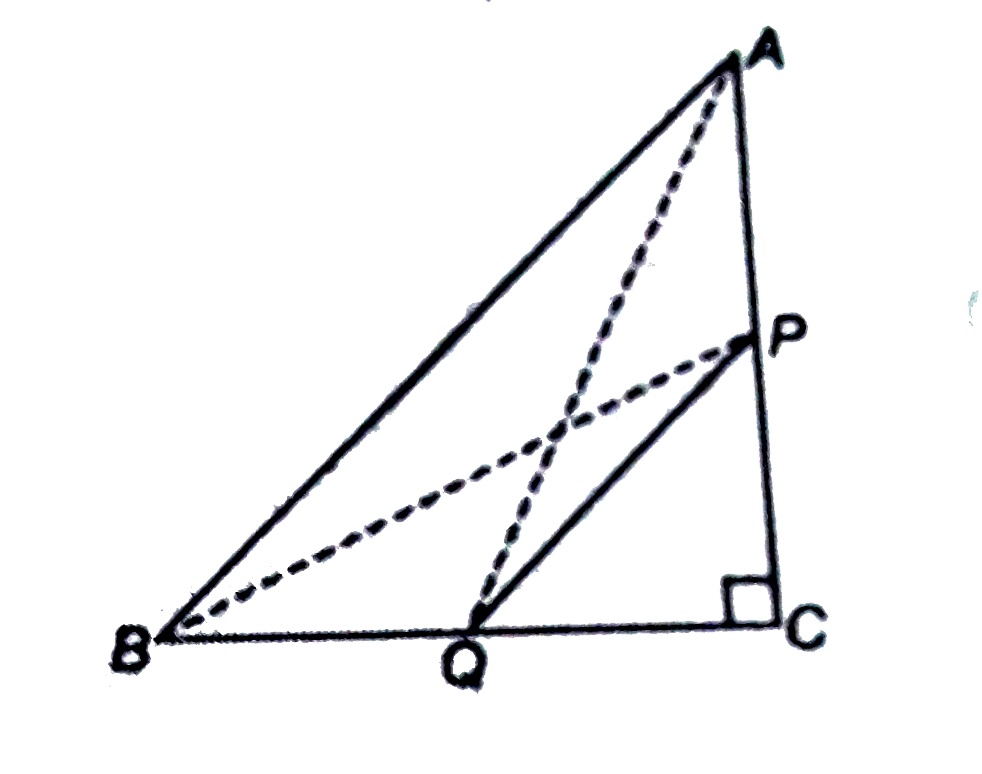
P and Q are the mid-points of the sides CA and CB respectively of a $△ A B C$ , right angled at C, prove that. (i) $4 A Q^{2} = 4 A C^{2} + B C^{2}$ (ii) $4 B P^{2} = 4 B C^{2} + A C^{2}$

Video Solution

Text Solution

Verified by Experts

(i) $△ A Q C, ∠ C = 90^{\circ}$
Using Pythagoras theorem
$A Q^{2} = A C^{2} + Q C^{2}$
$A Q^{2} = A C^{2} + {(\frac{B C}{2})}^{2}$
(Q is the mid-point of BC)
$A Q^{2} = A C^{2} + \frac{B C^{2}}{4}$
$4 A Q^{2} = 4 A C^{2} + B C^{2}$ …(1) Hence proved.
(ii) $△ B P C, ∠ C = 90^{\circ}$ ,
Using Pythagoras theorem, we have
$B P^{2} = B C^{2} + P C^{2}$ ,
$B P^{2} = B C^{2} + {(\frac{A C}{2})}^{2}$ (since P is the mid-point of AC)
$\Rightarrow 4 B P^{2} = 4 B C^{2} + A C^{2}$ ...(2) Hence proved.
(iii) Adding (1) and (2) we get
$4 A Q^{2} + 4 B P^{2} = 4 A C^{2} + B C^{2} + 4 B C^{2} + A C^{2}$
$4 (A Q^{2} + B P^{2}) = 5 (A C^{2} + B C^{2})$
$\Rightarrow 4 (A Q^{2} + B P^{2}) = 5 A B^{2} (A C^{2} + B C^{2} = A B^{2})$ Hence proved.

Updated on:21/07/2023