In Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
Step by step video, text & image solution for In Figure, A B C D is a parallelogram in which P is the mid-point of D C and Q is a point on A C such that C Q=1/4A Cdot If P Q produced meets B C at Rdot Prove that R is a mid-point of B Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6b
25 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIn figure, P is the mid-point of BC,,Q is the mid-point of AP , such that BQ produced meets AC at R. Prove that 3RA=CA
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
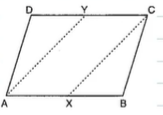
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
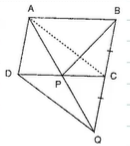
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
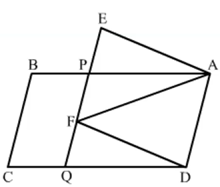
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View Solution
