In a △ABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ.
Step by step video, text & image solution for In a triangleABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6c
11 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6d
24 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A1/2(□ABCD)B1/3(□ABCD)C1/4(□ABCD)Dnone of theseIn a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A12(□ABCD)B13(□ABCD)C14(□ABCD)Dnone of theseABC is an equilateral triangle. P and Q are two points on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯AC respectively such that ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯¯BC. If ¯¯¯¯¯¯PQ=5cm, then area of ΔAPQ is :
A254 sq. cmB25√3 sq. cmC25√34 sq. cmD25√3 sq. cm
In △ABC, P and Q are the middle points of the sides AB and AC respectively. R is a point on the segment PQ such that PR: RQ =1: 2. If PR = 2cm, then BC =?
△ABC में, P और Q क्रमशः भुजाओं AB तथा AC के मध्य बिंदु हैं। R, PQ पर एक बिंदु इस प्रकार है कि PR: RQ =1: 2 यदि PR=2 सेमी, तो BC=
View SolutionIf DE||BC in △ABC where D and E are points on AB and AC respectively. If ADDB=815 and EC = 3.5 cm , find AE.
View SolutionIn ΔABC, P,Q and R are midpoints of sides AB,AC and BC respectively. Seg AS⊥BC and PQ || BR side BC. Prove that □ PQRS is a cyclic quadrilateral.
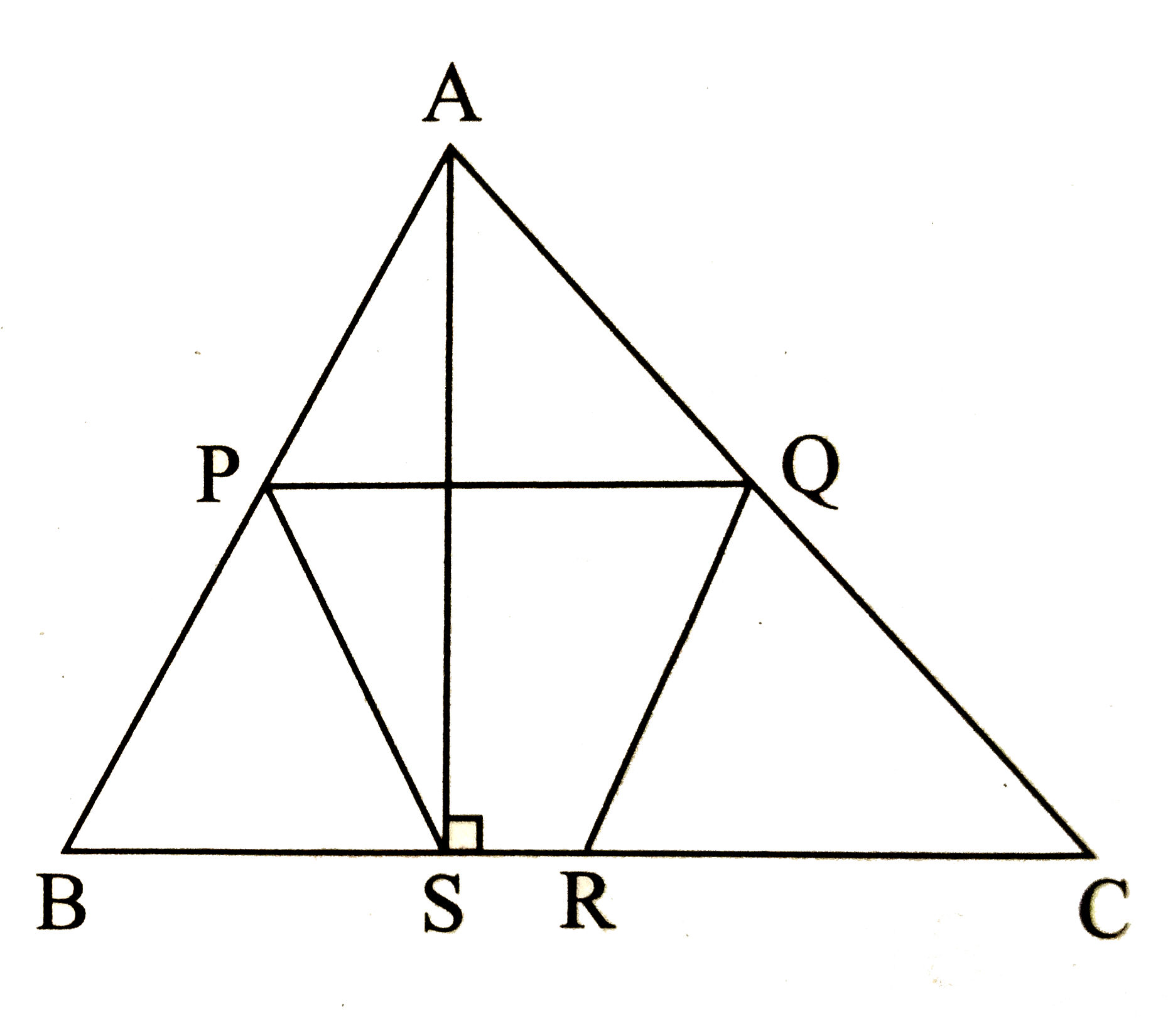
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionIn a ΔABC,AB=AC,PandQ are points on AC and AB respectively such that CB=BP=PQ=QA. if ∠AQP=θ, then tan2θ is a root of the equation
View Solution
