In ΔABC, P,Q and R are midpoints of sides AB,AC and BC respectively. Seg AS⊥BC and PQ || BR side BC. Prove that □ PQRS is a cyclic quadrilateral.
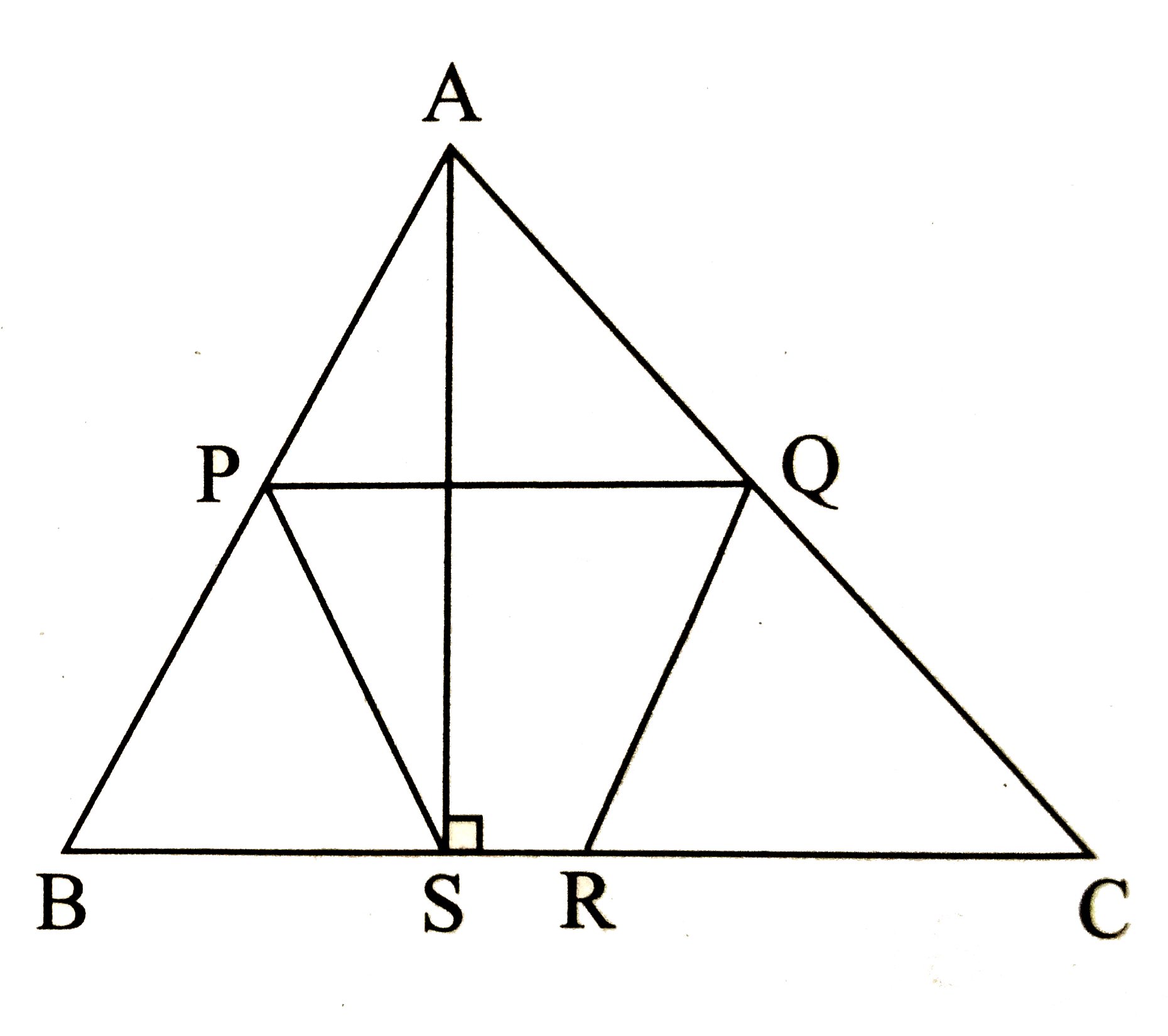
P and Q are the midpoints of sides AB and AC of ΔABC.
∴ by the midpoit theorem.
PQ∣∣BC ( i.e. BR ) and PQ =12BC …..(1)
BR=12BC ….( R is the midpoint of side BC ) …(2)
From (1) and (2),
PQ∣∣BR and PQ=BR.
∴□ PQRB is a parallelogram
∴∠B=∠Q ...(Opposite angles of a parallelogram ) ...(3)
In right angled triangle, median to the hypotenuse is half of the hypotenuse.
∴ in ΔABS,SP=12AB.
PB=12AB ...( P is the midpoint of side AB )
∴SP=PB
∴∠B=∠PSB ...( Isosceles triangle theorem ) ...(4)
From (3) and (4),
∠Q=∠PSB ....(5)
∠PSB+∠PSR=180∘ ....( Angles in a linear pair ) ...(6)
From (5) and (6)
∠Q+∠PSR=180∘
∴ by the converse of cyclic quadrilateral theorem , □ PQRS is a cyclic quadrilateral.
Topper's Solved these Questions
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:ASSIGNMENT 4.1
Explore 10 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:ASSIGNMENT 4.2
Explore 6 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:4.4 (1 mark each)
Explore 9 Videos
- CHALLENGING QUESTIONSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CHALLENGING QUESTIONSExercise:SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
Explore 1 Video
- COORDINATE GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:COORDINATE GEOMETRY Exercise:Assignment 6.5
Explore 13 Videos
Similar Questions
If ΔABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-
View SolutionIn a triangle ABC, P, Q and R are the midpoints of side BC, CA and AB respectively. If AC = 21 cm, BC = 29 cm and AB = 30 cm, then find the perimeter of the quadrilateral ARPQ
View Solution
Knowledge Check
P is any point on the side BC of a △ABC. P is joined to a. If D and E are the midpoints of the sides AB and AC respectively and M and N are the midpoints of BP and CP respectively then quadrilateral DENM is
Aa trapeziumBa parallelogramCa rectangleDa rhombusABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?A4√3cm2B8√3cm2C√3/3cm2D√3/4cm2
D and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?
View SolutionIn a △ABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionConsider a square OABC ,If P and Q are the midpoints of sides AB and BC ,respectively. Then the value of 2(AreaofΔOPQ)Areaof□OABC is
View Solution