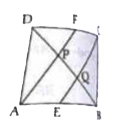
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

Given ,ABCD is a parallelogram
and since AB is parallel to CD
So,AE is also parallel to CF and AB=CD
AB=CD⇒AE=OF
So,in AECF
AE is parallel to CF and AE=CF
∵AF is parallel to CF
So,PF parallel to CQ and AP parallel to EQ
In,ΔDQC
F is the mid point of DC and PF is parallel to CQ
P is the mid point of DQ and,
=PQ=DP
Similarly, in ΔABP
E is the mid point of AB and AP is parallel to EQ
Q is the mid point of BP
PQ=QB
Thus,PQ=DP=BQ
Thus, the line segment AE & EC triset the diagonal BD.
Similar Questions
In a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
In Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionE and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View SolutionIn a parallelogram ABCD, points E and F are respectively midpoint of sides AB and CD (see the adjacent figure). Prove that line segment AF and EC trisect diagonal BD.
 View Solution
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH.
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
 View Solution
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).
 View Solution
View Solution

