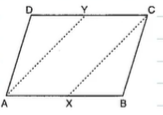
In Figure, ABCD
is a parallelogram. E
and F
are the mid-points of the sides AB
and CD
respectively. Prove that the line segments AF
and CE
triset (divide into three equal parts) the diagonal BD.

Step by step video & image solution for In Figure, A B C D is a parallelogram. E and F are the mid-points of the sides A B and C D respectively. Prove that the line segments A F and C E triset (divide into three equal parts) the diagonal B Ddot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.

View SolutionE and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View Solution