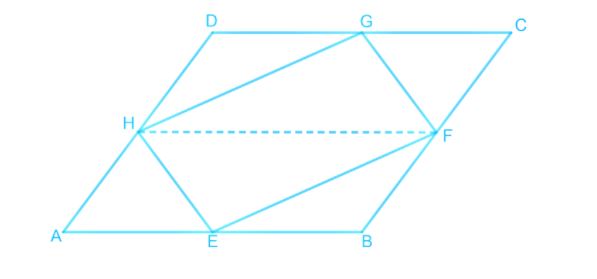
If $E, F, G$ and $H$ are respectively the mid-points of the sides of a parallelogram $A B C D,$ show that $a r (E F G H) = \frac{1}{2} a r (A B C D) .$

Video Solution

Text Solution

Verified by Experts

Let us join HF.
In parallelogram ABCD,
$A D = B C$ and $A D ∣ ∣ B C$ (Opposite sides of a parallelogram are equal and parallel)
$A B = C D$ (Opposite sides of a parallelogram are equal)
$\Rightarrow \frac{1}{2} A D = \frac{1}{2} B C$ and $A H ∣ ∣ B F$
$\Rightarrow A H = B F$ and $A H ∣ ∣ B F$ (Since H and F are the mid-points of AD and BC)
Therefore, $A B F H$ is a parallelogram.
Since $Δ H E F$ and parallelogram $A B F H$ are on the same base HF and between the same parallel lines AB and HF,
$∴ A r e a (Δ H E F) = \frac{1}{2} A r e a (A B F H)$ .....(1)
Similarly, $A r e a (Δ H G F) = \frac{1}{2} A r e a (H D C F)$ .....(2)
On adding Equations (1) and (2), we obtain
$A r e a (Δ H E F) + A r e a (Δ H G F) = \frac{1}{2} A r e a (A B F H) + \frac{1}{2} A r e a (H D C F)$ ...... (3)
From the figure, we can see that,
$A r e a (Δ H E F) + A r e a (Δ H G F) = A r e a (E F G H)$ ....... (4)
$\frac{1}{2} A r e a (A B F H) + \frac{1}{2} A r e a (H D C F) = \frac{1}{2} A r e a (A B C D)$ ..... (5)
From (3) & (4) and (5) we have,
$A r e a (E F G H) = \frac{1}{2} A r e a (A B C D)$

|

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile