In a parallelogram are any two points on the sides and respectively. Show that
and parallelogram ABCD
have same base between same
and parallelogram ABCD
have same base AD and between same lines
.
Topper's Solved these Questions
Similar Questions
Show that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms. GIVEN : A parallelogram ABCD.E and F are the mid-points of opposite sides AB and CD respectively. TO PROVE : ar(^(gm)AEFD)=ar(^(gm)EBCF) CONSTRCUTION : Join EF.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
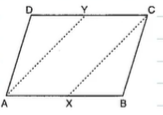View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionXY isa line parallel to side BC of ABC.BEA and CFAB meet XY in E and F respectively.Show that ar(ABE)=ar(ACF).
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionIn a ABC, D, E, F are the mi-points of sides BC, CA and AB respectively. If ar(ABC)=16cm2, then ar (trapezium FBCE)= 4 cm2 (b) 8 cm2 (c) 12cm2 (d) 10cm2
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
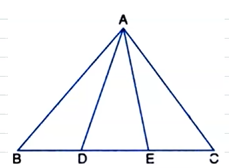View Solution