In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
If a student is selected at random, then the probability that he has passed the examination is
1/7
11/35
11/14
None of these
The correct Answer is:C
Let P(i) be the probability that exactly I students are passing an examination. Now given that
P(Ai)=λ2i(whereλis constant)
⇒10∑i−1P(Ai)=10∑i−1λi2=λ10×11×216=λ×386=1
⇒λ=1/358=5/77.
Let A reprsent the event that selected students have passed the examination. Therefore,
P(A)10∑i−1P(A/Ai)P(Ai)
=10∑i−1i10i2358
=1385010∑i−1i3
=102×1124×3850=1114
Now P(Ai/A)=(PA/Ai)P(Ai)P(A)
=1358×1101114
=111×55×15=13025
Topper's Solved these Questions
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - MATRIX MATCH TYPE
2 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - Exercise (Matrix)
8 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - Exercise (Multiple)
17 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - JEE Advanced Previous Year
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
Similar Questions
In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
If a students selected at random is found to have passed the examination, then the probability that he was the only student who has passed the examination is
View SolutionIn a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
The probability that exactly 5 students passing an examination is
View Solution
Knowledge Check
In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
If a students selected at random is found to have passed the examination, then the probability that he was the only student who has passed the examination isA1/3025B1/605C1/275D1/121In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
The probability that exactly 5 students passing an examination isA1/11B5/77C25/77D10/77Out of 80 students in a class , 30 passed in Mathematices , 20 in Electronics and 10 in both. If one students is selected at random . The probability that the has passed in none of the subject in
A35B14C32D14
In a class of 10 student, probability of exactly i students passing an examination is directly proportional to i2. If a student is selected at random, then the probability that he has passed the examination is
View SolutionThere are n students in a class. Ler P(Eλ) be the probability that exactly λ out of n pass the examination. If P(Eλ) is directly proportional to λ2(0≤λ≤n).
If a selected student has been found to pass the examination, then the probability that he is the only student to have passed the examination, is
View SolutionIn a medical examination of students of a class, the following blood groups are recorded.
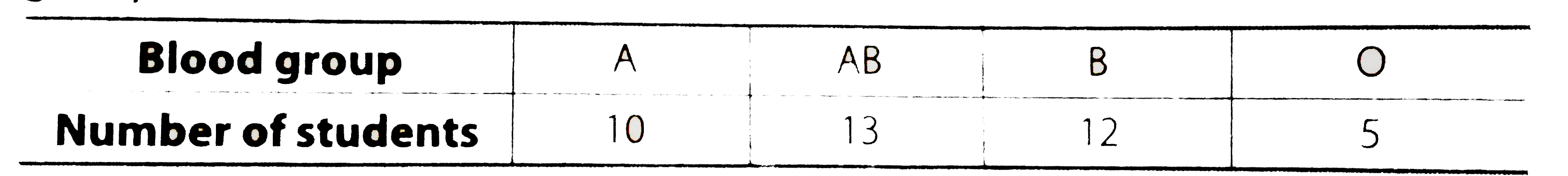
A student is selected at random from the class. The probability that he/she has blood group B, is
View SolutionThere are n students in a class. Ler P(Eλ) be the probability that exactly λ out of n pass the examination. If P(Eλ) is directly proportional to λ2(0≤λ≤n).
If a selected student has been found to pass the examination, then the probability that he is the only student to have passed the examination, is
View SolutionIn a medical examination of students of a class, the following blood groups are recoreded.
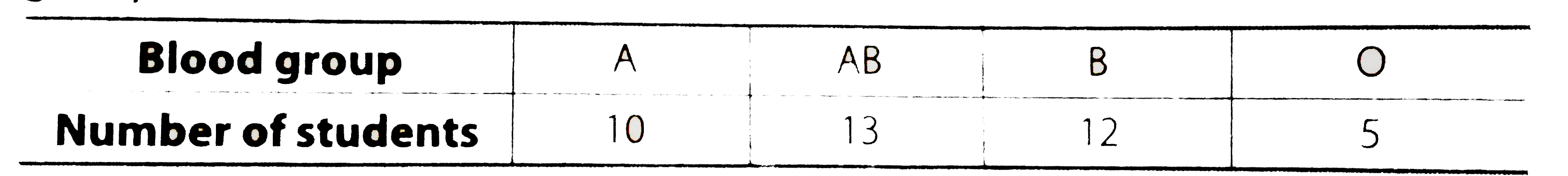
A student is selected at random from the class. The probability that he/she has blod group B, is
View Solution
