one vertex of the triangle of maximum area that can be inscribed in the curve |z−2i|=2 is 2+2i, then remaining vertices are
Step by step video & image solution for one vertex of the triangle of maximum area that can be inscribed in the curve |z-2i|=2 is 2+2i, then remaining vertices are by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If one vertex of the triangle having maximum area that can be inscribed in the circle |z−i|=5is3−3i , then find the other vertices of the triangle.
View SolutionIf one vertices of the triangle having maximum area that can be inscribed in the circle |z−i|=5 is 3-3i, then find the other verticles of the traingle.
View Solution
Knowledge Check
One vertex of the triangle of maximum area that can be inscribed in the curve |z−(1+i)|=2√2 is −2+2i, then the remaining vertices are
A(5−√32)+i(1+3√32)B(5−√32)+i(1−3√32)C(5+√32)+i(1−3√32)D(5+√32)+i(1+3√32)In a right angle triangle ABC , what is the maximum possible area of a square that can be inscribed whe one of its vertices coincide with the vertex of righ angle of the triangle ?
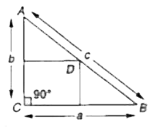AabBaba+bCa+babD(aba+b)2If z1,z2,z3 are the vertices of an equilateral triangle inscribed in the circle |z|=1 then the area of the triangle having z1,z2,z3 as its vertices is
A√32B√34C3√34DNone of these
A rectangle of maximum area is inscribed in the circle |z−3−4i|=1. If one vertex of the rectangle is 4+4i, then another adjacent vertex of this rectangle can be 2+4i b. 3+5i c. 3+3i d. 3−3i
View SolutionA rectangle of maximum area is inscribed in the circle |z−3−4i|=1. If one vertex of the rectangle is 4+4i, then another adjacent vertex of this rectangle can be a. 2+4i b. 3+5i c. 3+3i d. 3−3i
View SolutionFind the area of the greatest isosceles triangle that can be inscribed in the ellipse (x2a2)+(y2b2)=1 having its vertex coincident with one extremity of the major axis.
View SolutionIf 2,4,8 are the ordinates of the vertices of a triangle inscribed in the parabola y2=8x ,then area of triangle is
View SolutionIn a right angle triangle ABC, what is the maximum possible area of a square that can be inscribed when one of its vertex coincide with the vertex of right angle of the triangle?
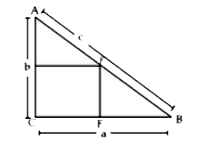
View Solution