In a right angle triangle ABC, what is the maximum possible area of a square that can be inscribed when one of its vertex coincide with the vertex of right angle of the triangle?
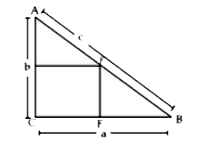
ab
aba+b
(a+bab)2
(aba+b)2
Step by step video & image solution for In a right angle triangle ABC, what is the maximum possible area of a square that can be inscribed when one of its vertex coincide with the vertex of right angle of the triangle? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
In a triangle ABC, right angled at B, then
View SolutionIn the given figure, in a right angle triangle ABC, AB=12cm and AC=15cm. A square is inscribed in the triangle. One of the vertices of square coincides with the vertex of triangle. What is the maximum possible area (in cm2) of the square ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a right angle triangle ABC , what is the maximum possible area of a square that can be inscribed whe one of its vertices coincide with the vertex of righ angle of the triangle ?
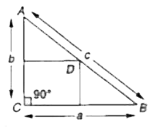 AabBaba+bCa+babD(aba+b)2
AabBaba+bCa+babD(aba+b)2 - Question 2 - Select One
If a right angled triangle ABC of maximum Δ area is inscribed in a circle of radius R , then
AΔ=2R2Br=(√2−1)RC1r1+1r2+1r3=√2−1RDs=(√2−1)R - Question 3 - Select One
An equilateral trinagle is inscribed in parabola y2=8x whose one vertex coincides with vertex of parabola.Find area of triangle.
A(196√3)B(194√3)C(192√3)D(190√3)
Find the area of the right angled triangle of least area that can be drawn so as to circumscribe a rectangle of sides 'a' and 'b', the right angle of the triangle coinciding with one of the angles of the rectangle.
View SolutionABC is a right angles triangle at B. The hypotenuse AC is four times the perpendicular BD drawn to it from the opposite vertex and AD
View SolutionWhat is the area of the largest rectangle that can be inscribed in a right angled triangle with legs oflength 3 and 4?
View SolutionThe maximum area of a right angled triangle with hypotenuse h is
View SolutionSide of an equilateral triangle inscribed in y2=4x such that one vertex of the triangle coincide with the vertex of parabola is
View Solution

