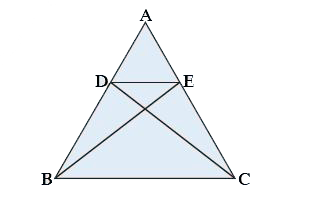
In the following Figure, D and E are two points on BC such that BD = DE = EC . Show that ar (ABD) = ar (ADE) = ar(AEC)
can you now answer the equation that you left in the "Introduction " of the capther, whether the filed of Budhia has been actually divided into three parts of equal area ? Solution in Kannada
The correct Answer is:3
Step by step video, text & image solution for In the following Figure, D and E are two points on BC such that BD = DE = EC . Show that ar (ABD) = ar (ADE) = ar(AEC) can you now answer the equation that you left in the "Introduction " of the capther, whether the filed of Budhia has been actually divided into three parts of equal area ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the Given figure, E is any point on median AD of a △ABC Show that ar (ABE) = ar (ACE)
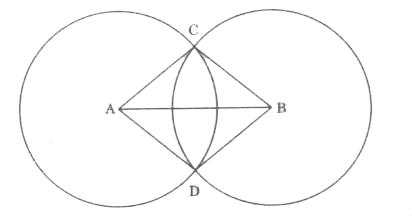
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two point of intersection.
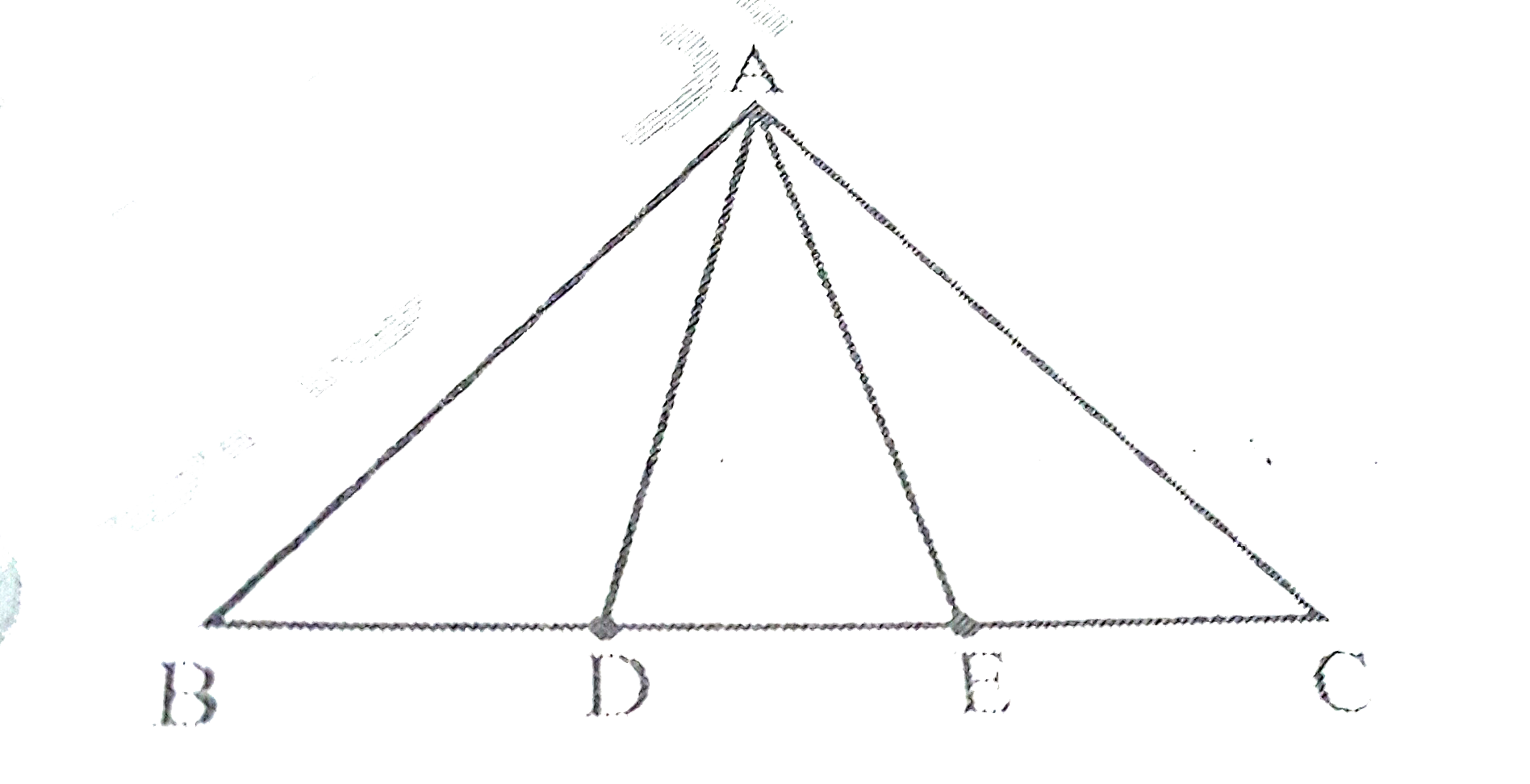
View SolutionIn Fig.30D and E are to points on BC such that BD=DE=EC. Show that ar(ABD)=ar(ADE)=ar(AEC)
View Solutionआकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित है कि BD=DE=EC है। दर्शाइए कि ar(ABD)=ar(ADE)=ar(AEC) है ।
क्या आप अब प्रश्न का उत्तर दे सकते है, जो आपने इस अध्याय की भूमिका में छोड़ दिया था कि क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागो में विभाजित हो गया है?
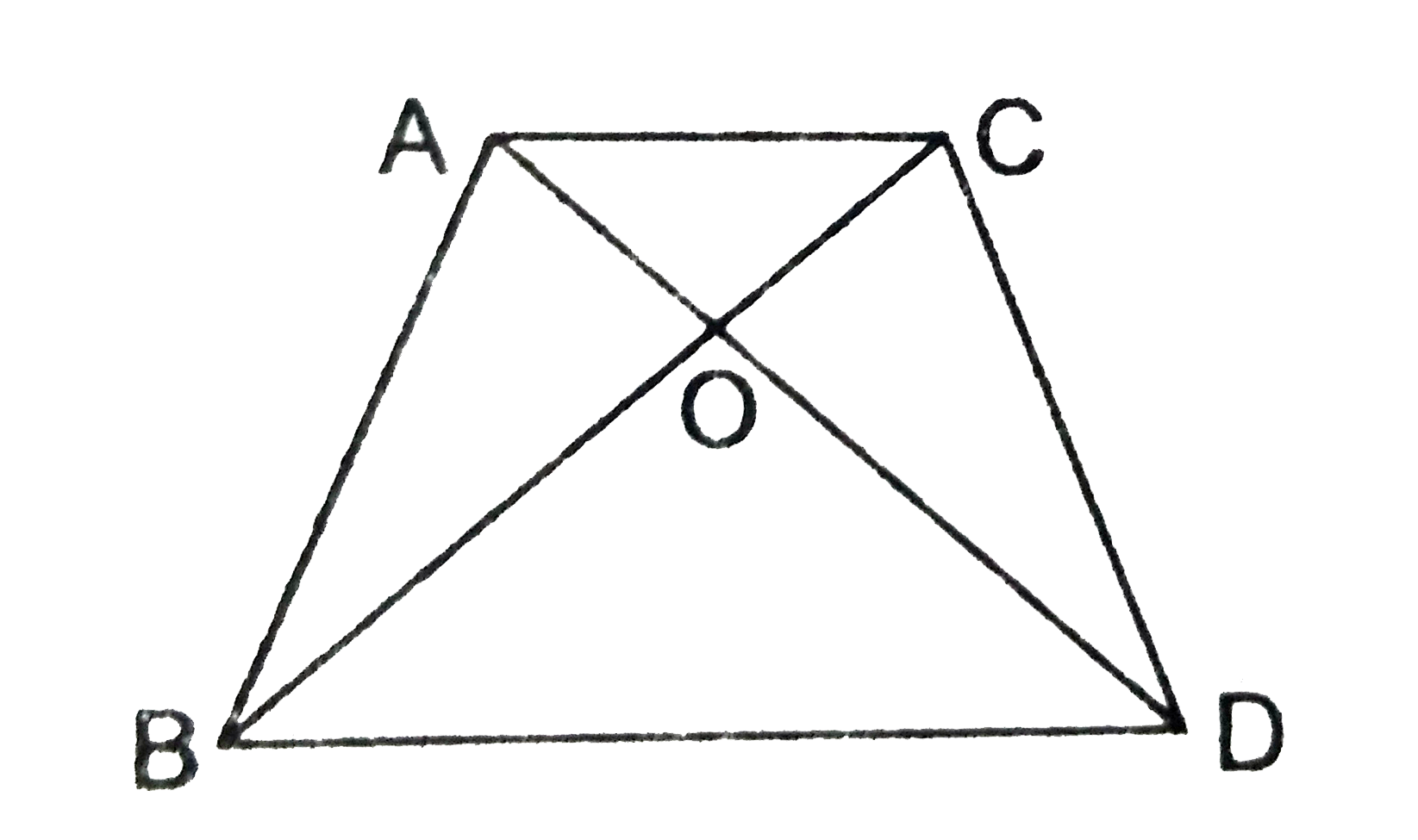
View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
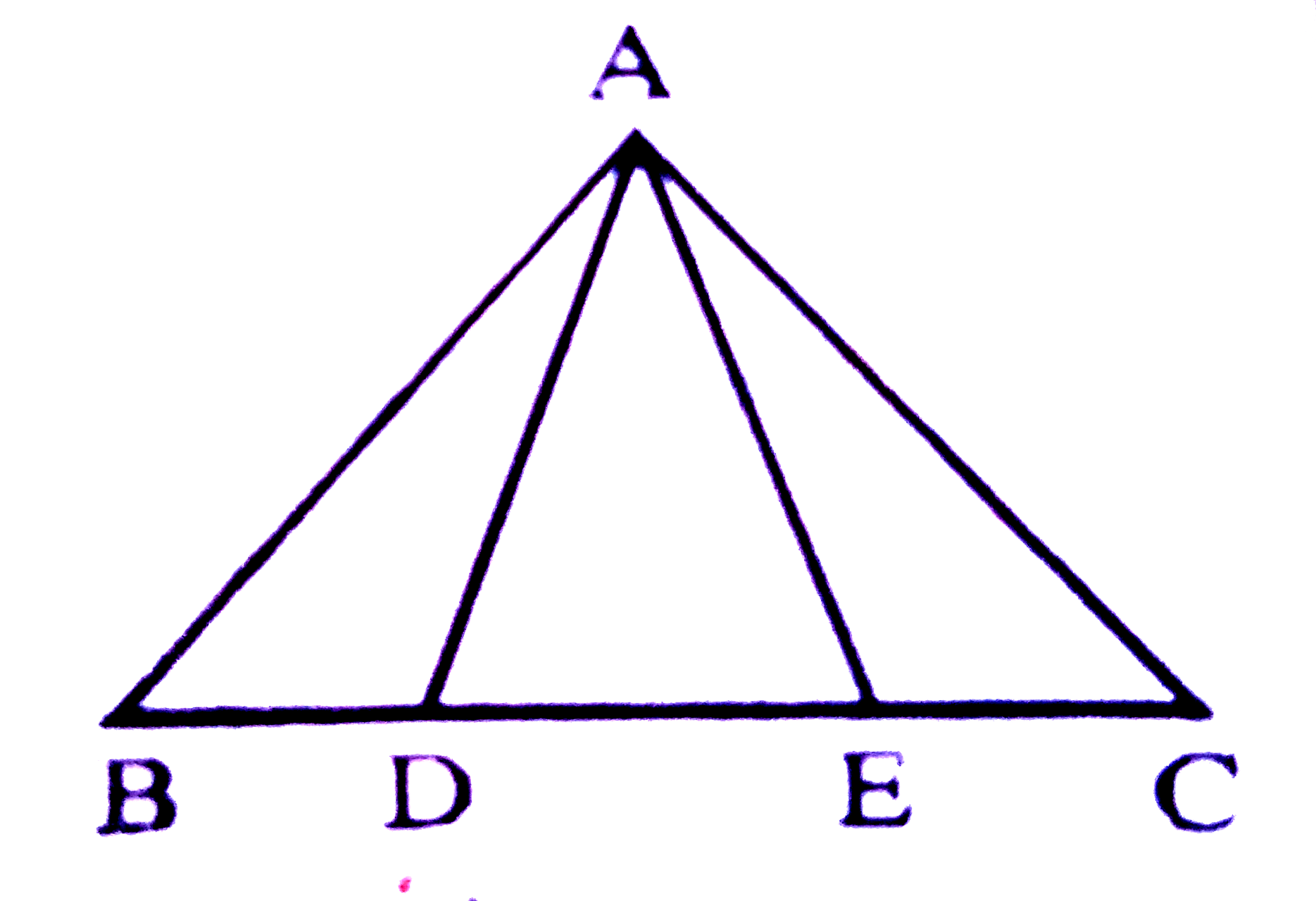
View Solutionआकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित है कि BD= DC= EC है। दर्शाइए कि ar (ABD) = ar (ADE) =ar (AEC) है।

View Solutionयदि ΔABC के आधार BC पर कोई बिंदु D लिया गया है तथा AD को E तक इस प्रकार आगे बढ़ाया गया है कि DE = AD , सिद्ध कीजिए कि
ar(ΔBCE)=ar(ΔABC)
View Solutionदिए गए चित्र में भुजा BC पर दो बिंदु D और E इस प्रकार स्थित है की BD=DE=EC है| दर्शाइए की
ar(ABD)=ar(ADE)=ar(AEC) है|
View SolutionIn, D and E are two points on BC such that BD = De = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the 'introduction' of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
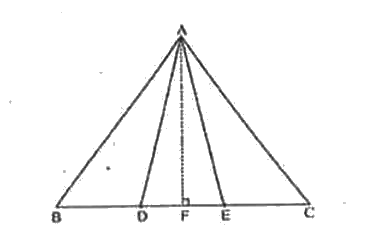
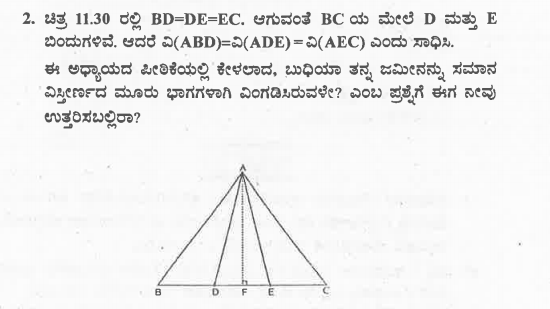
View Solutionಚಿತ್ರ ರಲ್ಲಿ BD = DE= EC, ಆಗುವಂತೆ BC ಯ ಮೇಲೆ D ಮತ್ತು E ಬಿಂದುಗಳಿವೆ. ಆದರೆ ವಿ(ABD)=ವಿ(ADE) =ವಿ(AEC) ಎಂದು ಸಾಧಿಸಿ. ಈ ಅಧ್ಯಾಯದ ಪೀಠಿಕೆಯಲ್ಲಿ ಕೇಳಲಾದ, ಬುಧಿಯಾ ತನ್ನ ಜಮೀನನ್ನು ಸಮಾನ ವಿಸ್ತೀರ್ಣದ ಮೂರು ಭಾಗಗಳಾಗಿ ವಿಂಗಡಿಸಿರುವಳೇ? ಎಂಬ ಪ್ರಶ್ನೆಗೆ ಈಗ ನೀವು ಉತ್ತರಿಸಬಲ್ಲಿರಾ?
View SolutionIn the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC)=ar(ΔEBC) . Prove that DE || BC.
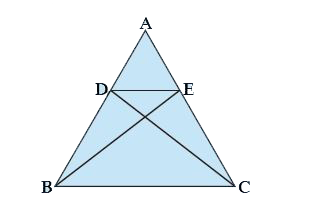
View SolutionIn the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC)=ar(ΔEBC) . Prove that DE || BC.
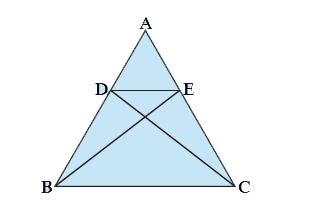
View SolutionDelta ABC A point D on BC is such that BD = ( 1)/( 3) DC Show that ar( Delta ABD ) = ( 1)/( 4) ar ( Delta ABC )
View SolutionIn the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC)=ar(ΔEBC) . Prove that DE || BC.
View SolutionIn the given figure DE∣∣BC. If AD=1.5cm, BD=2AD, then find ar(ΔADE)ar(trapezium BCED)
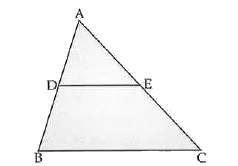
View Solution
