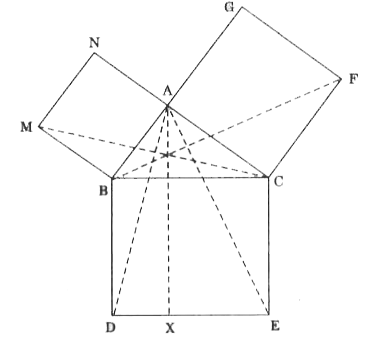
In the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX DE meets BC at Y. Show that
(i)
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv)
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
The correct Answer is:(i)
(ii)
(iii) AMBN
(iv)
(v) 2
(vi) ACFG
ABMN
Topper's Solved these Questions
Similar Questions
ABC is a right triangle right angled at A. BCED, ACFG and ABMN aresquares on the sides BC, CA and AB respectively. Line segment AX⊥DEmeets BCat Y. Show that:(i) ΔMBC≅ΔABD(ii) a r\ (B Y X D)\ =\ 2\
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN aresquares on the sides BC, CA and AB respectively. Line segment AX⊥DEmeets BCat Y. Show that:(i) ΔMBC≅ΔABD(ii) a r\ (B Y X D)\ =\ 2\
View Solution
Knowledge Check
- Question 1 - Select One
ABC is a right angled triangle right angled at Band∠A=60∘andAB=20cm , then the ratio of sides BC and CA is
A√3:1B1:√3C√3:√2D√3:2 - Question 2 - Select One
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ) - Question 3 - Select One
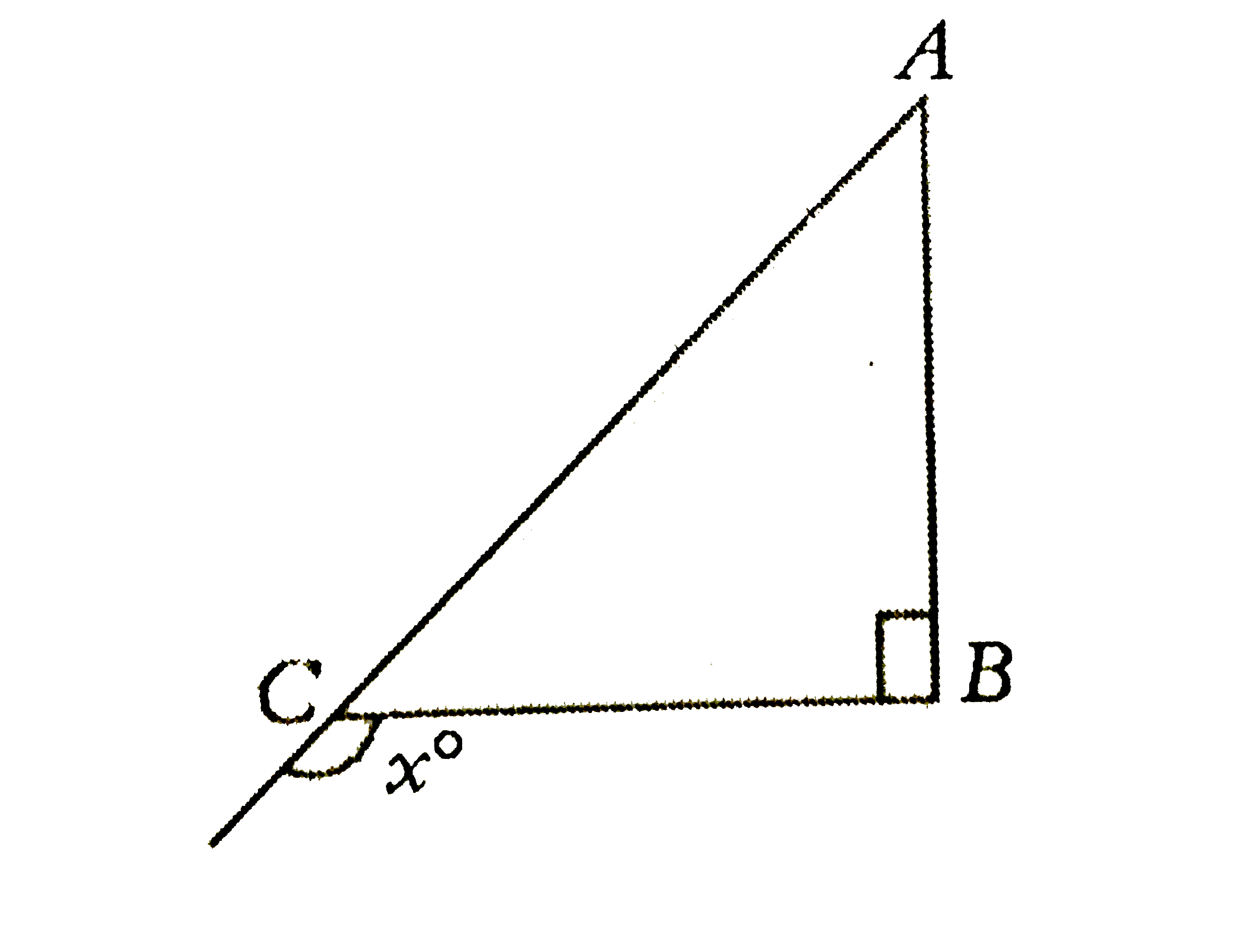
In the figure above, ABC is a right triangle and BC=AB , then find x∘.A45∘B90∘C120∘D135∘
ABC is a right triangle, right angled at C and AB=√2BC. Then, find ∠ABC.
View Solution
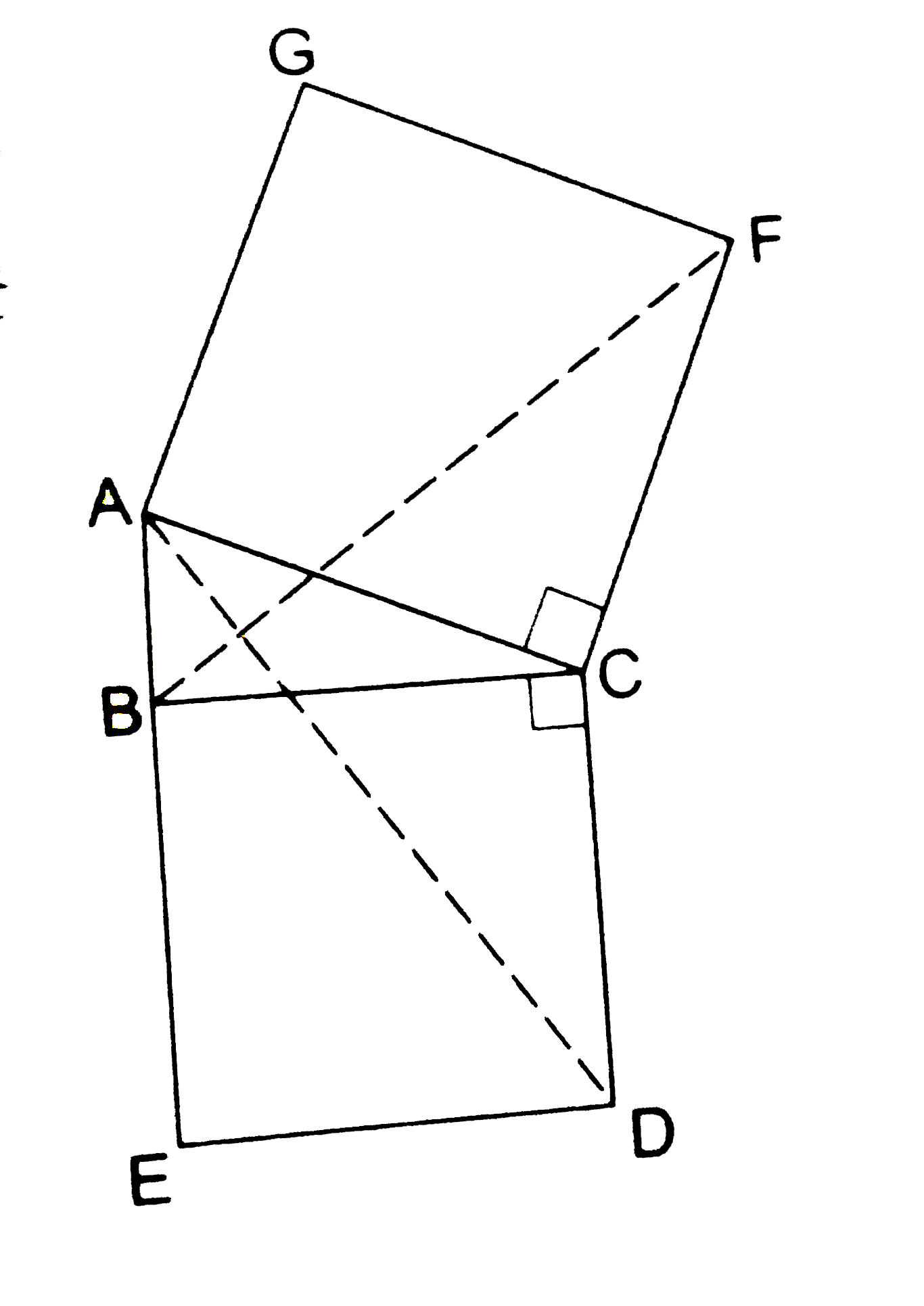
In the figure above, ABC is a right triangle and BC=AB , then find x∘.View SolutionIn the given figure, ABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = FB.
 View Solution
View SolutionABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = BF.
View SolutionABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = BF.
View Solution

