In Fig.9.29, ar (BDP) = ar (ARC)and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
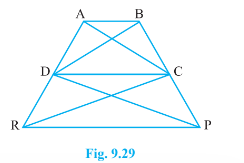
We have to prove quadrilaterals ABCD and DCPR are trapeziums.
It is given that Area(△DRC)=Area(△DPC)
As △DRC and △DPC are lying on the same base DC having equal areas, therefore, they must lie between the same parallel lines.
According to Theorem 9.3:
Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
DC∣∣RP
Therefore, DCPR is a trapezium.
It is also given that Area(△BDP)=Area(△ARC)
Now, subtract ar(△DPC) fromm ar(△BDP) and ar(△DRC) from ar(△ARC)
ar(△BDP)−ar(△DPC)=ar(△ARC)−ar(△DRC) [Since, ar(△DPC)=ar(△DRC)]ar(△BDC)=ar(△ADC)
Since △BDC and △ADC are on the same base CD having equal areas, they must lie between the same parallel lines. (According to Theorem 9.3)
AB∣∣CD
Therefore, ABCD is a trapezium.
Similar Questions
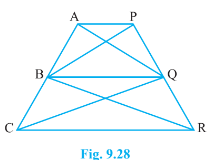
In Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).
 View Solution
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionProve that If each diagonal of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
 View Solution
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
 View Solution
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View Solution

